I am listening to the podcast 372 Pages We’ll Never Get Back. In episode 22-29 they discuss Tekwar.

372 Pages We’ll Never Get Back

Real or fanfic

The spreadsheet ! For the first time, the guessing skill was significantly better than flipping a coin! In 3 out of 6 episodes, all guesses were correct! Magnificent!

Summary of important advice

Consistency, continuity.

• Jake has no idea how Gomez got in / Jake (from his own perspective) gave him access recently.
• Anachronistic speech.
• It was Beth. But it wasn’t Beth.
• Jake hates androids. Jake finds android Beth beautiful. Jake calls her Beth.
• Complicated plan to get Jake where he was going anyway, almost killing him on the way.
• The cynical kid is suddenly naive and trusting.
• The hair of Gomez isn’t alive anymore. On the other hand, now he sounds like Swiers.

Be exciting. Have stakes.

• Sitting around and talking about people not there. Not action. Boring.
• First sentence in chapter: Jake woke up. Non-actiony.
• Mentioning a super interesting court case in passing only.
• 1st sentence: The aircar started to sputter. Flat.
• No stakes. Nobody’s using tek.

Flow. Chekhov’s gun.

• Suddenly a new conversation begins.
• Characters described in detail, but only appearing once.
• Hokori and Sands have been mentioned so many times and still haven’t appeared.
• We hear almost nothing about the tek war phenomenon.
• And then the big bad dies within seconds.
• Checkov’s password not used.

Originality.

• Stereotypical Mexico.
• A lot of crusty detectives.

Realism. Being human.

• Punishment = suspended animation? Rehabilitation?
• Print of various shapes. Triangular?
• Apparently the robot searched for information for 14 seconds and THEN said something. That’s a long time. And very specific.
• Odd dialogue to mention the year.
• They were ALWAYS razzing him? Because his father was THIN?
• Surprising your wife is a good idea.
• Noticing what’s usually there.
• In the future all areas will be sectors.
• A British robot in California.
• Jack is talking to himself, a lot.
• Noises from Jack’s own apartment? Draw a gun! Oh wait, it was just a vacuum starting at a weird time!
• Jack doesn’t understand the concept of recordings.
• Tapping out a very, very specific fantasy.
• Gomez’ hair is alive.
• His hair seemed to bounce.
• A colleague of Jake could clear his name, but wanted money first.
• Pointing upwards with the thumb.
• As you know, Bob. Persons telling each other what they already know. Instead of letting the narrator tell it.
• The term kamikaze isn’t well-known anymore.
• Slender, but pretty.
• 1940s movies are still well-known. Girl Friday.
• For 3 minutes the house is disappearing, and they just stand there.
• Do people leave forwarding addresses at hotels?
• Beth must be super hot. Universal agreement.
• Jake happens to know how to fix androids.
• Jake is really hurt by Beth sassing him.
• Both chrome and very life-like androids are available.
• Warbride whips up a mood and then stops.
• So many mechanical arms.

Variety.

• Robot printer, happens a lot.
• Repetition. All laughs sound weird.
• Stereotypes. Cab driver.
• Repetition. At what age did he marry?
• Repetition. The state of Chihuahua. The exact center/middle.
• Constant reminders we’re in Mexico.
• Keep repeating that Jake’s foot is booted.

Details: not too many, not too few.

• Chrome everything. Do we need to know the chrome man has a chrome brain? Keep reminding us.
• Some sort of smuggler. Assorted. Vague, shouldn’t have been mentioned in the first place.
• Apparently the robot searched for information for 14 seconds and THEN said something. That’s a long time. And very specific.
• Unsubtling: that coffin was where he slept.
• Wife’s full name, too much.
• Suicide committed suicide. Stop here?
• Including that the correct button was pushed.
• Noting a time period with a weird length and it wasn’t needed.
• She is naked. Also her shoulders are naked.
• If the wall had been there, he would have slammed into it.

POV. Tone.

• Gross. The hero craps his pants.
• Name, Hambrick, distracting, funny.
• Noir isn’t just talking about the darkness all the time.
• … said the robot pimp disdainfully.

Use words and phrases correctly.

• Calling something a sky or air (vehicle), with no explanation or significance.
• Something slightly resembles a laugh. What does it actually sound like?
• Lank, not lanky.
• Plas everything. Sounds futury, dumb.
• Pronunciation of lazgun?
• Where she stores her clothes is a habit.
• Shrugging one shoulder.
• Reinventing pleather.
• A lot of whilst.
• Italicized words are at this point fully integrated words from Spanish.
• Bad sentence structure. Adding amigo to a sentence in the wrong place. “It’s, amigo, a possibility worth mentioning.” “Until he showed up last night, I wasn’t even certain he hadn’t decided I was as crooked as everyone else thinks I am.”
• A quiet smile. They can be loud?
• Just adding moonbase at the beginning.
• Age = math exercise. ‘Jake said, “Hey, fifty-six isn’t that old. I’m little more than a half dozen years from there myself, Gomez.” ‘
• Xmas.
• A sentence changing pov and tense more than once.
• Not being consistent with whether plas-whatever is 1 or 2 words or hyphenated.
• Name, Hambrick, distracting, funny.
• Yes, but what color is licorice?
• Renaming cab to landcab.
• A quirky alley.
• Commence (used wrong), start, begin.
• So many commas.
• Bulbs of light.
• Going back and forth between human and cyborg.
• Place dialogue tag in the middle. “That sure isn’t,” complained Swiers, “going to help our case”.
• Using Warbride and Elana interchangeably.
• Passwords should be dramatic?
• Using tek to relive the path (as is or better) and create a better present. What else is there?
• Chinese in one sentence, Japanese in the next.

Other stuff

• Racism.
• Racist against robots AND Mexicans.

Ep. 22

Ranking.

1. Eye of Argon (most fun)
2. Cline

Ep. 23, ch. 1-7

Don’t do this

• Vehicles are sky or air. There’s a difference? What? Does it matter?
• Chrome everything. Do we need to know the chrome man has a chrome brain? Keep reminding us.
• Some sort of smuggler. Assorted. Vague, shouldn’t have been mentioned in the first place.
• Something slightly resembles a laugh. What does it actually sound like?
• Robot printer, happens a lot.
• Lank, not lanky.
• Punishment = suspended animation? Rehabilitation?
• Print of various shapes. Triangular?
• Apparently the robot searched for information for 14 seconds and THEN said something. That’s a long time. And very specific.
• Gross. The hero craps his pants.
• Unsubtling: that coffin was where he slept.
• Repetition. All laughs sound weird.
• Odd dialogue to mention the year.
• Plas everything. Sounds futury, dumb.
• Pronunciation of lazgun?
• They were ALWAYS razzing him? Because his father was THIN?
• Stereotypes. Cab driver.
• Racism.
• Surprising your wife is a good idea.
• Repetition. At what age did he marry?
• Noticing what’s usually there.
• In the future all areas will be sectors.
• A British robot in California.
• Jack is talking to himself, a lot.
• Noises from Jack’s own apartment? Draw a gun! Oh wait, it was just a vacuum starting at a weird time!
• Where she stores her clothes is a habit.
• Wife’s full name, too much.
• Shrugging one shoulder.
• Suddenly a new conversation begins.
• Suicide committed suicide. Stop here?
• Jack doesn’t understand the concept of recordings.
• Tapping out a very, very specific fantasy.
• Reinventing pleather.

Running gags

• Clinean.
• Ogden.

Oops.

• Odgen.

Real or fanfic, 44:22

• Mike guessing.
• Fanfic ✔️ Real ✔️ Fanfic ✔️ Fanfic ✔️

Ep. 24, ch. 8-11

Don’t do this

• Sitting around and talking about people not there. Not action. Boring.
• Jake has no idea how Gomez got in / Jake (from his own perspective) gave him access recently.
• A lot of whilst.
• Italicized words are at this point fully integrated words from Spanish.
• Gomez’ hair is alive.
• His hair seemed to bounce.
• A colleague of Jake could clear his name, but wanted money first.
• Bad sentence structure. Adding amigo to a sentence in the wrong place. “It’s, amigo, a possibility worth mentioning.” “Until he showed up last night, I wasn’t even certain he hadn’t decided I was as crooked as everyone else thinks I am.”
• Pointing upwards with the thumb.
• As you know, Bob. Persons telling each other what they already know. Instead of letting the narrator tell it.
• A quiet smile. They can be loud?
• Just adding moonbase at the beginning.
• Age = math exercise. ‘Jake said, “Hey, fifty-six isn’t that old. I’m little more than a half dozen years from there myself, Gomez.” ‘
• Xmas.
• First sentence in chapter: Jake woke up. Non-actiony.
• Including that the correct button was pushed.
• A sentence changing pov and tense more than once.
• Not being consistent with whether plas-whatever is 1 or 2 words or hyphenated.
• Name, Hambrick, distracting, funny.
• The term kamikaze isn’t well-known anymore.
• Yes, but what color is licorice?
• Slender, but pretty.
• 1940s movies are still well-known. Girl Friday.

Running gags

• Long pauses in dialogue.
• Seemed to.
• Talking to himself.
• Settle down.
• Nobody laughs normally.
• Fuzzy.

Oops.

• Self-correction is actually fine.

Real or fanfic, 55:35

• Mike guessing
• Fanfic ❎ Fanfic ✔️ Real ❎ Real ✔️ Fanfic ✔️

Ep. 25, ch. 12-15

Don’t do this

• Characters described in detail, but only appearing once.
• Noir isn’t just talking about the darkness all the time.
• Mentioning a super interesting court case in passing only.
• For 3 minutes the house is disappearing, and they just stand there.
• Renaming cab to landcab.
• Stereotypical Mexico.
• Racist against robots AND Mexicans.
• A lot of crusty detectives.
• Do people leave forwarding addresses at hotels?
• A quirky alley.
• Beth must be super hot. Universal agreement.
• Commence (used wrong), start, begin.

Running gags

• Meetings.
• Discreet openings.
• Doing nothing for minutes.
• Living hair.

Oops.

• Missed the explanation for which parts of the house are real.
• Cyborg and robot, not the same.

Real or fanfic, 58:10

• Mike guessing
• Fanfic ✔️ Fanfic ❎ Fanfic ❎ Real ❎ Fanfic ✔️

Ep. 26, ch. 16-21

Don’t do this

• 1st sentence: The aircar started to sputter. Flat.
• Anachronistic speech.
• Noting a time period with a weird length and it wasn’t needed.
• It was Beth. But it wasn’t Beth.
• Jake hates androids. Jake finds android Beth beautiful. Jake calls her Beth.
• Jake happens to know how to fix androids.
• She is naked. Also her shoulders are naked.
• So many commas.
• Repetition. The state of Chihuahua. The exact center/middle.
• Bulbs of light.
• Jake is really hurt by Beth sassing him.
• Constant reminders we’re in Mexico.
• Hokori and Sands have been mentioned so many times and still haven’t appeared.

Running gags

• Hot daughter.
• Settle down.
• Discreet openings.
• Ogden.
• Shatlard.
• A variety of classic 80s dance moves.

Oops.

• The 1st time a word was shortened was not. The actual 1st was pop(ulation).
• Taking charisma for beauty?
• Talking about the programming of an android, when she’s simply an upload of the real Beth and should talk like her.
• Odgen.
• Deus ex knacks.

Real or fanfic, 39:34

• Mike guessing
• Fanfic ✔️ Real ✔️ Fanfic ✔️ Real ✔️ Fanfic ✔️

Ep. 27, ch. 22-26

Don’t do this

• Complicated plan to get Jake where he was going anyway, almost killing him on the way.
• Keep repeating that Jake’s foot is booted.
• Going back and forth between human and cyborg.
• Both chrome and very life-like androids are available.
• Place dialogue tag in the middle. “That sure isn’t,” complained Swiers, “going to help our case”.

Running gags

• Odgen.
• Shatlard.

Real or fanfic, 41:47

• Mike guessing
• Real ✔️ Fanfic ✔️ Fanfic ✔️ Fanfic ✔️ Fanfic ✔️

Ep. 28, ch. 27-30

Don’t do this

• Warbride whips up a mood and then stops.
• So many mechanical arms.
• Using Warbride and Elana interchangeably.
• No stakes. Nobody’s using tek.
• Passwords should be dramatic?
• We hear almost nothing about the tek war phenomenon.
• Using tek to relive the path (as is or better) and create a better present. What else is there?

Running gags

• The sweating fat man.
• The exact center.
• Dialogue tag in the middle.
• Odgen.
• Lag.
• John Candy. Non sequitur.

Oops.

• She’s part cyborg.

Real or fanfic, 49:17

• Mike guessing
• Fanfic ❎ Fanfic ✔️ Real ❎ Fanfic ✔️ Real ✔️

Ep. 29, ch. 31-end

Don’t do this

• The cynical kid is suddenly naive and trusting.
• … said the robot pimp disdainfully.
• Chinese in one sentence, Japanese in the next.
• If the wall had been there, he would have slammed into it.
• And then the big bad dies within seconds.
• The hair of Gomez isn’t alive anymore. On the other hand, now he sounds like Swiers.
• Checkov’s password not used.

Running gags

• Settle down.
• Curing cancer in 1 sentence.

Oops.

• Not knowing the expression “tumble to”. Or keen as a verb.

A fanfic earlier was a rewrite of bits from the book. 😦

Quality: Between Cline and Theis.

1. Eye of Argon (most fun)
2. Tekwar
3. Cline

This week the #puzzle is: Let’s Make a Tic-Tac-Deal! #probabilities

The game of Tic-Tac-Deal 2.0 has a 3-by-3 square grid with the numbers 3 through 11, arranged as follows:

3 4 5 6 7 8 9 10 11

You start by rolling a standard pair of six-sided dice and add the two numbers rolled. You place an X on the board on the square that contains the sum. If the sum is a 2 or 12, or if you roll a sum that you have previously rolled, then your roll is wasted.

If you have exactly three rolls of the dice, what are your chances of getting three Xs in a row (either horizontally, vertically, or diagonally)?

And for extra credit:

In the actual game, you get five rolls instead of three. But as before, rolling a 2, a 12, or a number that you have already rolled is a wasted turn.

With five rolls of the dice, what are your chances of getting three Xs in a row, either horizontally, vertically, or diagonally?

Let’s Make a Tic-Tac-Deal!

Highlight to reveal (possibly incorrect) solution:

Program

I’m in a hurry this week, so I just monto carloed this one.

 3 rolls, accumulated probability = 0.05806
 4 rolls, accumulated probability = 0.18999
 5 rolls, accumulated probability = 0.36138
 6 rolls, accumulated probability = 0.52770
 7 rolls, accumulated probability = 0.66560
 8 rolls, accumulated probability = 0.76980
 9 rolls, accumulated probability = 0.84440
10 rolls, accumulated probability = 0.89594
11 rolls, accumulated probability = 0.93079
12 rolls, accumulated probability = 0.95404
13 rolls, accumulated probability = 0.96941
14 rolls, accumulated probability = 0.97959
15 rolls, accumulated probability = 0.98632

For the case with 3 rolls, I also did the math directly.

3-4-5	2	3	4	24
6-7-8	5	6	5	150
9-10-11	2	3	4	24
3-6-9	2	5	4	40
4-7-10	3	6	3	54
5-8-11	2	5	4	40
3-7-11	2	6	2	24
5-7-9	4	6	4	96
				452

E.g., for the first row, for every possible roll with 2 dice (there are 36), 2 of them have a sum of 3, 3 of them have a sum of 4 and 4 of them have a sum of 5. These 3 numbers multiplied give 24. All the numbers in the right column, multiplied by 3!/36³, are probabilities. The summed probability is therefore 0.0581275720164609, rounded to 0.058128. This checks out.

This week the #puzzle is: When Will You Cross Your Path? #geometry #angle

Anita the ant is going for a walk in the sand, leaving a trail as she goes. First, she walks 1 inch in a straight line. Then she rotates counterclockwise by an angle 𝝋, after which she walks another 2 inches. She rotates counterclockwise an angle 𝝋 again, after which she walks 3 inches. She keeps doing this over and over again, rotating counterclockwise an angle 𝝋 and then walking 1 inch farther than she did in the previous segment.

At some point during her journey, she crosses over her initial 1-inch segment. By “cross over,” I am including the two end points of that first segment.

Anita realizes that 𝝋 was the smallest possible angle such that she crossed over her 1-inch segment. (Among the ants, she’s known for her mathematical prowess.)

How long was the segment along which she first crossed over the 1-inch segment? Your answer should be a whole number of inches.

And for extra credit:

It’s time for you to check Anita’s work. What was the measure of angle 𝝋?

Remember, this was the smallest possible angle for each turn such that she crossed over her 1-inch segment at some later point.

When Will You Cross Your Path?

Highlight to reveal (possibly incorrect) solution:

Desmos. Image 1. Image 2.

My method is to recreate Anita’s path in Desmos and play around with it. Along the way I captured a couple of interesting images. When trying to find the angle, I zoomed in and added digits, until I thought I had enough.

Solutions: The segment is 4 inches long. The angle is 138.59°.

I am listening to the podcast 372 Pages We’ll Never Get Back. In episode 19-21 they discuss Eye of Argon.

372 Pages We’ll Never Get Back

Real or fanfic

The spreadsheet !

Summary of important advice

Consistency, continuity.

• Willing prostitutes. The unwilling quit.
• Untold agony = a disheartened emotion.
• Stating an angry remark.

Be exciting. Have stakes.

• Very long descriptions of what the soldiers are wearing.

Flow. Chekhov’s gun.

• Flashback not clearly marked.
• Physiology, sleeping, eating.

Realism. Being human.

• Impossible facial expressions.
• Hitting between the balls.
• How can they bear to live under such oppression?

Variety.

• Repetition of mount (horse). Wench.
• Ovals. Eyes, heads etc.
• A lot of lips.

Details: not too many, not too few.

• A lot of adjectives.
• After an indiscriminate period…
• Long, visual description, but hard to picture.
• Beady grey organs of sight.

POV. Tone.

• So many adverbs.
• Not just using “said”.
• Seemingly… Author, don’t you know?

Use words and phrases correctly. Punctuation.

• So many typos. Including in the fantasy words.
• How to pronounce Grignr.
• To shine dully.
• Who/what smells foul?
• A lot of commas, not clarifying.
• A lithe and opaque nose.
• She questioned?
• Dickered with the notion.
• Plural of shaman is shamen?
• Impossible to decode the sentences.
• The loincloth turned into a G-string.
• Changing tense.
• Pig in one sentence, dog in the next.

Ep. 19

MST3K for eye of argon .

Ep. 20, ch. 1-4

Don’t do this

• So many typos. Including in the fantasy words.
• How to pronounce Grignr.
• A lot of adjectives.
• To shine dully.
• Repetition of mount (horse). Wench.
• Flashback not clearly marked.
• Who/what smells foul?
• A lot of commas, not clarifying.
• Willing prostitutes. The unwilling quit.
• A lithe and opaque nose.
• Ovals. Eyes, heads etc.
• She questioned?
• Stating an angry remark.
• After an indiscriminate period…
• Dickered with the notion.
• Long, visual description, but hard to picture.
• Plural of shaman is shamen?
• Untold agony = a disheartened emotion.
• Physiology, sleeping, eating.
• Beady grey organs of sight.

Running gags

• Hell of a rig.
• An alien observing and describing human behaviour.
• Bulging sinews, see a doctor.
• After an indiscriminate period…

Oops.

• Conan the Barbarian uses slut a certain way?

Real or fanfic, 58:36

• Mike guessing
• Fanfic ✔️ Fanfic ✔️ Real ❎ Fanfic ❎ Fanfic ❎ Real ❎

Ep. 21, ch. 5-end

Don’t do this

• Impossible facial expressions.
• So many adverbs.
• Hitting between the balls.
• Impossible to decode the sentences.
• Very long descriptions of what the soldiers are wearing.
• The loincloth turned into a G-string.
• The tediously honed pelvis of the rodent.
• Changing tense.
• Not just using “said”.
• Seemingly… Author, don’t you know?
• How can they bear to live under such oppression?
• Pig in one sentence, dog in the next.
• A lot of lips.

Running gags

• Ovals.
• Sluts.
• Writing in a hurry.

Oops.

• Thinks the ergonomic mallet was a cup.
• Have read the afterword, missed the mention of Conan?

I juli var vi på ferie i #Viborg. Her besøgte vi bl.a. toget.

Lang togtur.

Jeg tog et par billeder gennem vinduerne. Jeg blev bl.a. optaget af, at en skov kan danne en slags skyline, sådan en takket linje mod himlen.

Og dermed er min reportage fra sommerferien slut!

I juli var vi på ferie i #Viborg. Her besøgte vi bl.a. alle mulige små steder, der ikke får deres egen side.

Tidligt eksperimenterede vi med at finde kiosker, hvor de solgte den lokale avis. Det betød bl.a. en tur til sygehuset. Selve sygehuset så interessant ud. Og jeg glemte fuldstændig at fotografere det, så her er en kollage af andres billeder.

Viborg har et lille tog, der fungerer som en hop-on-hop-off bus. Med 2 stop. Men der bliver fortalt om de interessante steder undervejs, så den er god nok. Vi brugte den på en halv tur, mest fordi vi havde ondt i benene.

Diverse landskab (bl.a. en bakke), og en sky. Og nogle blomsterdimser, der pyntede rundt omkring og muligvis er lavet af plastic.

Og ikke apropos noget som helst: Manglende evne til at stave eller Når Man Bliver Vildført Af AI/OCR. (Der står Trykke. Hvad burde der have stået??? Og hvor mange stavefejl får du det til? Men vi elsker dig naturligvis alligevel, Elias .) Og et forkert gæt på en bogtitel. (Deltageren gættede B, det var C.)

I am listening to the podcast 372 Pages We’ll Never Get Back. In episode 9-16 they discuss Armada.

372 Pages We’ll Never Get Back

Real or fanfic

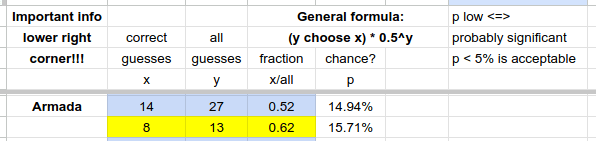
The spreadsheet !

Summary of important advice

Consistency, continuity.

• Yawnsville the young man said.
• There’s an important difference between young Clark Kent and young Luke Skywalker?
• Claiming a group of real people made a game, when they don’t have the skills.
• The reasonable people are also villains.
• Mom uses a lot more time than is possible.
• The keying of a car is (not) very visible.
• Feels Star Wars fandom is embarrasing, then immediately forgets it.
• Claiming Edge of Tomorrow and Avatar can be crossed in a meaningful way.
• Being surprised when the same thing happens again.
• Humans are just apes. Oh wait, we’re not.
• Going from being shallow to caring deeply about the planet.
• Being in a hurry, but waiting for the other guy to turn around a corner.
• Anachronisms.
• Weak jokes, big laughs.
• People have learned something earth shattering, and they behave normally.
• Zack thinks some sf movies are bad?
• To my surprise I did something, I’ve done many times before.
• Is it power leap or power jump?
• Rocky Balboa does not sound like a person from Philadelphia.
• He detects irony, but it’s also lost on him.
• Dad had psychological issues, but wasn’t fired.
• Star Trek and Wars are important, but neither are really about aliens invading Earth.
• Admiral Akbar famously IDENTIFIES traps.
• Happily nodding while so many people just died.
• It makes no sense, I understand it perfectly.
• Society is mentioned, but it was actually 3 people.
• The swastika in the beginning was stupid, the aliens are smart.

Be exciting. Have stakes.

• A lot of pages, almost no plot.
• A list of years and events.
• Boring controllers.
• A fictitious ad.
• Someone playing a game.
• An unboxing.
• Battle cry: Let’s do diz.
• Show, don’t tell.
• But I’m agnostic! Simply don’t mention it.
• Lengthy recap of battle.
• Big news, father is alive, and it’s just said, dryly. Unforced error.
• Pregnant pause + stand for an awkward beat.
• Stereotypes.
• Repetition of phrases. Glance. Enormous x 2 in 1 sentence. Video.
• A list of snacks.
• All the letters from dad are included. No surprises.
• Description of battle, not engaging.
• Boring: navigating through menus.
• Repetition of words. Contorted (face). That playlist.
• Cliché ending.

Flow. Chekhov’s gun.

• Lex ex machina.
• Heavy or clumsy foreshadowing.

Originality.

• Flat out stealing Terminator.
• Stealing valor. Quotes by great people.

Realism. Being human.

• Eating 1 pop-tart?
• 18-years old and spitballs.
• Boy finds stack of video games, reads diary.
• Boy is satisfied with explanation for how dad died, but then turns 10.
• 10-years-olds have guilty pleasures?
• How many back to back to back viewings?
• The government controlled the ENTIRE video game industry?
• Dumb joke amused him EVERY TIME.
• Children like being bored by adults.
• My mom is insanely hot.
• My mother would protect me with heavy weaponry.
• Close to graduating high school, but has no plans.
• Just teenagers in general.
• Defending against aliens isn’t a team sport?
• The aliens move in very predictable 4/4 rhythms.
• Out of body. I heard myself gasp.
• That Hollywood plan was bad.
• High school seniors know they have father figures?
• Zack’s eating meatloaf, mom tries to slow him down every few minutes.
• A very long line in a conspiratorial voice.
• The voices of Sagan and James Earl Jones are wonderful/evil.
• Everything is either memorized or almost forgotten.
• Synchronized screaming.
• There’s a standard Nintendo controller?
• “Boom!” the 18-year-old said.
• Emotions bouncing around.
• Zack destroys a valuable ship, and the admiral is playfully sarcastic.
• Oh, and your father is a crybaby, said the admiral.
• The attack is in 5 hours! Also, here’s a uniform.
• Token Asian.
• A talks, all the time B is chuckling.
• People taking forever to recognize known motion.
• Zack doesn’t recognize praying.
• Very disdainful towards religion.
• Debbie has no answer to an attack on her religion.
• He missed that he might die???
• Feeling like a list of things.
• Everybody’s afraid, but father is delighted.
• Suddenly we’re in a hurry.
• Isolated people doing fine and making jokes.
• Being very surprised that father and son look alike.
• Suddenly sounding like Wodehouse.
• Every second counts and there’s time to talk hobbies.
• Soldiers shouldn’t have time for hobbies.
• You got my reference. Goofy grin.
• Dad’s mood swings.
• Zack can interpret all expressions.
• The admiral is very informal.
• Zack can identify fine bone china.
• Zack knows his own little tics.
• Even the new guy has given up on an error he just heard for the first time.
• The 3 top guys think there might be a conspiracy?
• Why all the secrecy?
• It doesn’t make sense dad makes this joke. Everybody makes the same kinds of joke all the time. Everybody’s the same person.
• Keep the war on drugs going until this gamer weed is perfected.
• Everybody’s so horny.
• How did Lex get promoted that fast?
• Gallows humor isn’t a well known word?
• Not checking the gym for people before shooting the roof.
• Long fingers. (Zack’s mom.)
• “Is that a tricorder?” End scene. (Was that a joke?)
• Being impressed by HD. On a small screen.
• Screaming for a long time.

Variety.

• New book, exactly the same style.
• Spitballs in school, cliché.
• A lot of Star Wars references.
• 2 Star Wars references close together.
• Repetition, cyclopean.
• Everything is instant. Everything is a million. Everything is exactly like… Make it smaller.

Details: not too many, not too few.

• Making a subtle reference, then immediately saying more.
• Excalibur, too much.
• Nobody wondered whether you lived close to school.
• Nobody wondered about eyewitnesses.
• An avatar controlling a drone, hard to visualize.
• Explaining what a taunt is.
• Revealing an incident, that was easy to guess.
• Comparing a shape to Arecibo, not very well known.
• Bad physical descriptions. Hard to imagine.
• When did they see the shuttles? When they were there.
• Oh, it’s your first moon quake?
• Rushed chapters, abrupt ending.
• A lot happens in 1 sentence, could be a separate book.
• How rankings work.
• And that was all it took.
• Seconds later: Reports are coming in.
• In 1 sentence: Clean abundant energy. Cures for cancer.

POV. Tone.

• … as it came to be known. When is the narrator?
• The narrator doesn’t know what is going on.
• Calling something a fun fact, when it’s not fun. And during a serious section.
• Comparing a battle to Christmas lights, popcorn and beer cans. Not very battle-y.

Use words and phrases correctly.

• The distant horizon.
• Using the same unusual word in 2 consecutive sentences.
• How should sobrukai glaive be pronounced?
• Cold pop-tarts are raw?
• The retro outfit was retro from day 1?
• What’s a Garp phase?
• Wanderlust.
• An actor nails a role, that was original.
• We went to their moon AND we have the home team advantage.
• It looked exactly like (what it was).
• I had never been so glued to a screen.
• People of Europa = Europans, confusing.
• Calling something a power leap.
• WTF. I nodded in agreement.
• … power lines like Godzilla. Mangled sentence.
• Almost as if. Which I actually had. (It only feels like a simulation.)
• I wish we’d met a long time ago, said the teenager.
• … but … Not contradictory.
• Wrong name, book of revelations.
• Seeing 20/20 out of the corner of his eye.
• Radiant doesn’t mean that.
• How to write out the Close Encounters melody.
• Not just using the word “said”.
• Mom was FOND of pointing out his gaydar was broken, OFTEN.
• Consistently calling a ship shaped like a dodecahedron a dodecahedron. It had 3 names!
• Being reminded of something that is exactly the same.
• Blushing visibly.
• Gross:
  • Sired.
  • Woman described in a creepy way.

Ep. 9

Review or review, 9:20

• Mike guessing
• RP1 ❎ Armada ✔️ RP1 ✔️? Armada ✔️ RP1 ❎

Real or fanfic, 19:57

• Mike guessing
• Fanfic ❎ Fanfic ✔️

Mike wants to some day do an Ernest Hemingway contest, just for Cline.

Ep. 10, ch. 1-3

Don’t do this

• In general: the style is painfully similar to that of rp1.
• A lot of pages and almost no plot.
• Distant horizon. Unnecessary word.
• Using the same word in 2 consecutive sentences.
• Yawnsville. Are you Fonzie?
• The sobrukai glaive. Pronunciation? Jerry Lewis!
• Eating 1 pop-tart?
• Cold pop-tarts are raw?
• Making a subtle reference and then unsubtling it.
• The retro outfit was retro from day 1?
• Spitballs. Clichés. Sounds too young.
• Excalibur, too many details.
• Answering an unasked question. Distance between school and home.
• Saying there’s an important difference between a young Clark Kent and a young Luke Skywalker.
• What’s a Garp phase?
• Sired. Gross.
• Boy finds a stack of games and reads a diary instead.
• Boy thinks a few details of father’s death were enough, but then he turned 10.
• Literally a list of years and events. Boring. No comments.
• 10-year-olds have guilty pleasures?
• How many back to back viewings, doing nothing else?
• The government controlled the ENTIRE video game industry?
• Wanderlust?
• That the tie fighter is involved in the naming AND LOOK of the Thai restaurant? Absurd.
• Dumb joke amused him EVERY TIME.
• Children like being bored by adults?
• Play a game where an avatar controls a drone.
• Boring controllers. And an ad for a fictitious store. Someone playing a game. And then an unboxing.
• Claiming a game was made by real world people without the needed skills.
• Stealing too much: This is Terminator.

Running gags

• Hauling ass?
• Rush is back!

Oops.

• No, the episode isn’t 6 hours long.

Real or fanfic, 27:00

• Mike guessing
• Fanfic ✔️ Real ✔️

Ep. 11, ch. 4-7 (until phase 2)

Don’t do this

• My mother is insanely hot.
• My mother would protect me with heavy weaponry. Really?
• The reasonable people are depicted as villains. Like his grandmother who didn’t like, that his mother dated a loser.
• His mother works, goes out to dance and watches a lot of television. When?
• He’s close to finishing high school and have no plans?
• Self awareness without taking action. Being embarrassed by his Star Wars fandom, but then keeps talking about it lovingly.
• Assuming people don’t know what taunts are.
• Not accurately depicting teenagers now.
• An actor nails an original part.
• Defending against aliens isn’t a team sport?
• We went to their moon AND we have the home team advantage.
• Layers of simulation. Hard to picture.
• Detailed description of a video game session.
• Battle cry: let’s do diz.
• The aliens move in very predictable 4/4 rhythms.
• The keying of the car is very noticeable but also not.
• Revealing an incident, that was very easy to guess.
• There’s no doubt, but eyewitnesses are important.
• How do we cross Edge of Tomorrow and Avatar?
• I heard myself gasp.
• He’s surprised by the spaceships, again.
• The Hollywood plan was bad.
• High school seniors know they have father figures?
• His real name is… Yawn.
• It looked exactly like what it was.

Running gags

• A lot of back to back viewings.
• Insert hot before mom.
• Rigs.
• Observing oneself doing stuff.
• It seemed like an eternity. (But it wasn’t.)

Oops.

• “Where they live” only means something literally?

Real or fanfic, 37:22

• Mike guessing
• Hint: 1 is real
• Fanfic ✔️ Fanfic ❎ Fanfic ✔️ Real ❎
• Conor guessing
• Fanfic ✔️ Fanfic ✔️ Real ✔️ Fanfic ✔️

Ep. 12, ch. 8-11 (to 12)

Don’t do this

• Humans are just apes. Oh, wait, we’re not.
• Going from being shallow to caring deeply about the planet.
• Clichés.
• Zack’s eating meatloaf, mom tries to slow him down every few minutes.
• A very long line in a conspiratorial voice.
• Make sure references are crystal clear.
• A lot of Star Wars references.
• Being in a hurry, but waiting for the other guy to turn around a corner.
• Woman described in a creepy way.
• Anachronisms.
• Weak jokes, big laughs.
• People have learned something earth shattering, and they behave normally.
• Repetition, cyclopean.
• The voices of Sagan and James Earl Jones are wonderful/evil.
• Everything is either memorized or almost forgotten.
• Show, don’t tell.
• I had never been so glued to a screen.
• Zack thinks some sf movies are bad?
• People of Europa = Europans, confusing.
• Synchronized screaming.
• There’s a standard Nintendo controller?
• But I’m agnostic! Simply don’t mention it.
• Calling something a power leap.
• WTF. I nodded in agreement.

Running gags

• Pendergast.
• Not in control of ones own faculties.
• Hot mom.
• Clinean: What if I won’t do it? You’ll be drafted. I will? No.
• Rig in scrotum.
• A female of the species.
• Glaive.
• Like a… No, it IS a…

Real or fanfic, 28:27

• Conor guessing
• Fanfic. ✔️ Real. ❎ Fanfic. ✔️
• Mike guessing
• Fanfic. ✔️ Fanfic. ✔️ Fanfic. ❎ Real. ✔️

Spoken word performance about “apes”: Dance, Monkeys, Dance .

Ep. 13, ch. 12-15 (up to 16)

Don’t do this

• … as it came to be known. When is the narrator?
• The narrator doesn’t know what is going on.
• Calling something a fun fact, when it’s not fun. And during a serious section.
• To my surprise I did something, I’ve done many times before.
• “Boom!”
• Heavy or clumsy foreshadowing.
• Emotions bouncing around.
• 2 Star Wars references close together.
• Everything is instant. Everything is a million. Everything is exactly like… Make it smaller.
• … power lines like Godzilla. Mangled sentence.
• Is it power leap or power jump?
• Lengthy recap of battle.
• Was it my imagination? Hm.
• Keep on trucking. Anachronisms.
• Almost as if. Which I actually had. (It only feels like a simulation.)
• Zack destroys a valuable ship, and the admiral is playfully sarcastic.
• Big news, father is alive, and it’s just said, dryly. Unforced error.
• Oh, and your father is a crybaby.
• The attack is in 5 hours! Also, here’s a uniform.
• Thank Zod?
• I wish we’d met a long time ago, said the teenager.
• Token Asian.
• Pregnant pause + stand for an awkward beat.
• A talks, all the time B is chuckling.
• Stereotypes.
• … but … Not contradictory.
• Rocky Balboa does not sound like a person from Philadelphia.
• People taking forever to recognize known motion.
• Zack doesn’t recognize praying.
• Very disdainful towards religion.
• Debbie has no answer to an attack on her religion.
• Wrong name, book of revelations.
• He missed that he might die???
• Comparing a shape to Arecibo, not very well known.
• Seeing 20/20 out of the corner of his eye.
• He detects irony, but it’s also lost on him.
• Feeling like a list of things.
• Everybody’s afraid, but father is delighted.
• Sci fi theft!
• Suddenly we’re in a hurry.
• Radiant doesn’t mean that.

Running gags

• … as it came to be known.
• Pendergast.
• This is like (forgettable movie).
• Repeating information in back to back sentences.
• Pregnant pause. Cline, take it easy. Also, settle down.
• Seemed to.
• Glaive.

Oops.

• Just doesn’t like that a flier jinked.

Real or fanfic, 30:05

• Mike guessing.
• Fanfic ❎ Real ❎ Fanfic ✔️ Fanfic ✔️

March 28th is Guntober.
Snake ‘n Bacon.

Picture of Daedalus:

Ep. 14, ch. 16-18 (up to 19)

Don’t do this

• Isolated people doing fine and making jokes.
• Overexplaining references.
• Repetition of phrases. Glance. Enormous x 2 in 1 sentence. Video.
• Stereotypical Asian.
• Being very surprised that father and son look alike.
• Suddenly sounding like Wodehouse.
• Every second counts and there’s time to talk hobbies.
• Soldiers shouldn’t have time for hobbies.
• You got my reference. Goofy grin.
• Dad’s mood swings.
• Zack can interpret all expressions.
• A list of snacks.
• Bad physical descriptions. Hard to imagine.
• The admiral is very informal.
• Zack can identify fine bone china.
• When did they see the shuttles? When they were there.
• Zack knows his own little tics.
• Even the new guy has given up on an error he just heard for the first time.
• The 3 top guys think there might be a conspiracy?
• Why all the secrecy?
• All the letters from dad are included. No surprises.
• Dad had psychological issues, but wasn’t fired.
• Star Trek and Wars are important, but neither are really about aliens invading Earth.
• Admiral Akbar famously IDENTIFIES traps.
• How to write out the Close Encounters melody.
• 250 pages. Still no plot.
• It doesn’t make sense dad makes this joke. Everybody makes the same kinds of joke all the time. Everybody’s the same person.
• Stealing valor. Quotes by great people.

Running gags

• Hot mom.
• Remember when our parents died?

Oops.

• Pronunciation of Das Boot.
• “Mispronouncing something wrong.”
• No, the episode isn’t 10 hours long.
• European/Europan.
• Yes, decahedron was corrected to dodecahedron. But it’s still described as a ten-sider with triangular faces.
• There are other ways to recognize a 20-sided shape than counting faces.

Real or fanfic, 44:22

• Mike guessing
• Fanfic ✔️ Fanfic ❎ Fanfic ✔️ Fanfic ❎ Fanfic ✔️ Real ❎
• Conor guessing
• Real ❎ Fanfic ❎ Fanfic ❎ ? Note that the 1st is Cline, but not Armada.

Inacronym, inaccurate acronym.
A clip will be posted, like hot dogs?
Live show coming up, will be recorded. (No, it won’t, unfortunately.)

Ep. 15, ch. 19-21 (up to phase 3)

Don’t do this

• The alien invasion still hasn’t begun!
• Keep the war on drugs going until this gamer weed is perfected.
• Not just using the word “said”.
• Mom was FOND of pointing out his gaydar was broken, OFTEN.
• Everybody’s so horny.
• How did Lex get promoted that fast?
• Gallows humor isn’t a well known word?
• Description of battle, not engaging.
• Comparing a battle to Christmas lights, popcorn and beer cans. Not very battle-y.
• Oh, it’s your first moon quake?
• I stab at thee, the Khan quote.
• Consistently calling a ship shaped like a dodecahedron a dodecahedron. It had 3 names!
• Boring: navigating through menus.

Running gags

• Golf ball atop a shot glass.
• Lag.
• Hauling ass.

Oops.

• Forgot Whoadie is a Shakespeare fan, or at least watched a lot of it.

Real or fanfic, 41:35

• Conor guessing
• Fanfic ✔️ Fanfic ✔️ Fanfic ✔️ Real ❎
• Mike guessing
• Fanfic ✔️ Fanfic ❎ Fanfic ✔️ Fanfic ❎ Real ❎

Ep. 16, ch. 22-end

Don’t do this

• Rushed chapters, abrupt ending.
• A lot happens in 1 sentence, could be a separate book.
• Lex ex machina.
• Happily nodding while so many people just died.
• Not checking the gym for people before shooting the roof.
• Long fingers. (Zack’s mom.)
• Repetition of words. Contorted (face). That playlist.
• “Is that a tricorder?” End scene.
• Being reminded of something that is exactly the same.
• Being impressed by HD. On a small screen.
• It makes no sense, I understand it perfectly.
• Blushing visibly.
• How rankings work.
• Screaming for a long time.
• And that was all it took.
• Seconds later: Reports are coming in.
• Cliché ending.
• Society is mentioned, but it was actually 3 people.
• The swastika in the beginning was stupid.
• In 1 sentence: Clean abundant energy. Cures for cancer.

Running gags

• Goods and services.
• Long fingers.
• Hot mom.
• Remember when our parents died?

I juli var vi på ferie i #Viborg. Her besøgte vi bl.a. Kongens Bar.

Kongens Bar (åbnet nærmest 5 minutter før vi kom ) lå rigtig belejligt for os. Så vi besøgte den hyppigt. En enkelt gang fik vi aftensmad (jægergryde, mums), og ellers prøvede vi deres drinks. Vi kom der tit nok til, at vi fik sludret lidt mere med personalet.

I juli var vi på ferie i #Viborg. Her besøgte vi bl.a. Fru Thomsen.

Fru Thomsen (åbnet i 2022 ) var kommet ind på min radar. De fokuserer på frokost, deriblandt tarteletter. Og det er så sjældent man får en god tartelet. Så det skulle prøves.

På billedet nedenfor ligger Fru Thomsen til venstre.