My previous post #ThisMonthsScienceNewsPuzzle, 20260116 is now public.

My previous post #ThisMonthsScienceNewsPuzzle, 20260116 is now public.

This week the #puzzle is: Can You Brighten Up the Room? #geometry #trigonometry #angles #reflection #animation
| While dining at a restaurant, I notice a lamp descending from the ceiling, as shown in the diagram below. The lamp consists of a point light source at the center of a spherical bulb with a radius of 1 foot. The top half of the sphere is opaque. The bottom half of the sphere is semi-transparent, allowing light out (and thus illuminating my table) but not back in. The light source itself is halfway up to the ceiling—5 feet off the ground and 5 feet from the ceiling. The ground reflects light. |
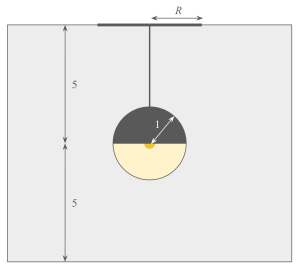 |
| Above the light, on the ceiling, I see a circular shadow. What is the radius R of this shadow? |
And for extra credit:
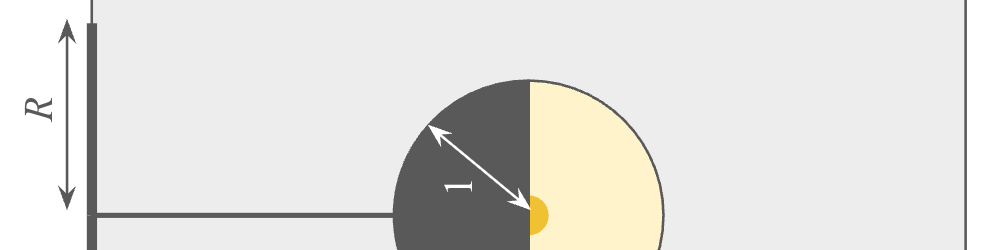
| Now suppose the lamp has a radius r and is suspended a height h off the ground in a room with height 2h. Again, the radius of the shadow on the ceiling is R. |
| For whatever reason, the restaurant’s architect insists that she wants r, h, and R, as measured in feet, to all be whole numbers. What is the smallest value of R for which this is possible? |
Thoughts:
Thoughts:
Ahem.
This actually assumes r = 1. Let’s try again.
My program finds several possible solutions.
| r: 40 | h: 52 | R: 65.0000 |
| r: 80 | h: 85 | R: 136.0000 |
| r: 80 | h: 104 | R: 130.0000 |
| r: 112 | h: 200 | R: 175.0000 |
| r: 120 | h: 156 | R: 195.0000 |
| r: 160 | h: 170 | R: 272.0000 |
| r: 160 | h: 208 | R: 260.0000 |
| r: 200 | h: 260 | R: 325.0000 |
| r: 224 | h: 400 | R: 350.0000 |
| r: 240 | h: 255 | R: 408.0000 |
| r: 240 | h: 312 | R: 390.0000 |
| r: 280 | h: 364 | R: 455.0000 |
| r: 320 | h: 340 | R: 544.0000 |
| r: 320 | h: 416 | R: 520.0000 |
| r: 360 | h: 468 | R: 585.0000 |
| r: 400 | h: 425 | R: 680.0000 |
Oh, and I did an animation of some of the solutions. Baby’s first animation.
From this I find, that R = 65 feet is the smallest solution.
This month the #puzzle is: Math puzzle: The homesick rover #addition #sum
| Far away, on a large, rocky exoplanet, a rover from Earth has just arrived on a mission of exploration. But the poor thing doesn’t want to explore. The moment it begins moving, it grows homesick and wants nothing more than to return to the very spot where it began. Unfortunately, it has received very explicit instructions. The first day, it must travel one kilometer forward in a straight line, then turn 90 degrees. The second day, it must travel two kilometers forward, then turn 90 degrees. The third day, it must travel three kilometers forward, then turn 90 degrees. The fourth day, it must travel four kilometers forward, then turn 90 degrees. And so on, for the duration of an eight-day mission. |
| The rover wants to return to the site where it landed. But it can choose only which direction to turn, left or right, at the end of each day. How can the rover end the eight-day mission back at its landing site? |
And as a bonus:
| A hundred rovers with the same set of instructions have been sent to other large, rocky planets, each with a different mission length, ranging from one day to 100 days. |
| How many of these rovers can end their missions back at their landing sites? |

Math puzzle: The homesick rover ![]()
Thoughts:
Thoughts:
Let’s look at the general case for odd numbers.
Now let’s look at the even numbers.
Putting the 2 rules together:
Let’s write this another way.
| n | x | y(+1) | Result |
| 1 | fail | fail | |
| 2 | fail | fail | |
| 3 | fail | fail | |
| 4 | fail | fail | |
| 5 | fail | fail | |
| 6 | fail | fail | |
| 7 | 2 | 3+1 | success |
| 8 | 2 | 4 | success |
| 9 | fail | fail | |
| 10 | fail | fail | |
| 11 | 3 | fail | fail |
| 12 | 3 | fail | fail |
| 13 | fail | fail | |
| 14 | fail | fail | |
| 15 | 4 | 7+1 | success |
| 16 | 4 | 8 | success |
| 17 | fail | fail | |
| 18 | fail | fail | |
| 19 | 5 | fail | fail |
| 20 | 5 | fail | fail |
This develops into a pattern. These work:
Let’s look at one of the actual problems in the Moscow Mathematical Papyrus.

Nowadays we would have a formula:
And of course we would have drilled school children in this formula, because everybody needs to know these things. Next we would have defined, for this particular problem, some values:
We’re not used to writing values with fractions like that in our time, so we need to convert that.
Now we can plug these values in.
And calculate.
You have found it correctly!
For some time now I have been trying to understand the Moscow Mathematical Papyrus. And for me, understanding = writing and sharing. Therefore the results of my thoughts are now available on this page.
What is this particular papyrus? Well, it’s math problems and solutions. Some of its importance hinges on “did they know how to do that already?” This goes for problems 10 and 14 especially. They knew how to calculate the area of a sphere? And the volume of a pyramid? Well, apparently, yes. They could also work with unknowns and take square roots. Exciting!
At some point the papyrus ended up in Moscow, and a lot of research was done on it at that time.

Without further ado, welcome to my treatment of the Moscow Mathematical Papyrus.
This week the #puzzle is: Some Coffee With Your Tea? #summation
| I have two glasses, one containing precisely 12 fluid ounces of coffee, the other containing precisely 12 fluid ounces of tea. |
| I pour one fluid ounce from the coffee cup into the tea cup, and then thoroughly mix the contents. I then pour one fluid ounce from the (mostly) tea cup back into the coffee cup, and then thoroughly mix the contents. |
| Is there more coffee in the tea cup, or more tea in the coffee cup? |
And for extra credit:
| I have two glasses that can hold a maximum volume of 24 fluid ounces. Initially, one glass contains precisely 12 fluid ounces of coffee, while the other contains precisely 12 fluid ounces of tea. |
| Your goal is to dilute the amount of coffee in the “coffee cup” by performing the following steps: |
| – Pour some volume of tea into the coffee cup. – Thoroughly mix the contents. – Pour that same volume out of the coffee cup (i.e., into the sink), so that precisely 12 fluid ounces of liquid remain. |
| After doing this as many times as you like, in the end, you will have 12 ounces of liquid in the coffee cup, some of which is coffee and some of which is tea. In fluid ounces, what is the least amount of coffee you can have in this cup? |

I’m not quite sure what happened with the magic squares. I guess the method I found (writing code to calculate equations and choose among primes) didn’t work. Ah well.
I was actually part of the way with the extra credit. N has to be even. N can’t be 18 or more. But then I would have gotten it wrong, by saying N = 4 wouldn’t work.
Thoughts:
Desmos 1 ![]() 2
2 ![]()
Throughts:
I’ve done Everybody Codes, back in November.

The Song of Ducks and Dragons [ 2025 ] ![]()
All my code is available ![]() . And so are my times. And I really like, that we operate with local times here.
. And so are my times. And I really like, that we operate with local times here.
.........................................................................................#
.................#...........#.....#........#........#.....#...........#.................#
.....#..##.#..#..#.#...#..#..#.....#...#.#..#..#.#...#.....#..#..#...#.#..#..#.##..#.....#
.#####.###.#.###.#.###.#####.#.#####.###.#.###.#.###.#####.#.#####.###.#.###.#.###.#####.#
##########################################################################################
Quest 16. There’s a certain kind of wall, with a connection between a list of numbers, a given length and the resulting wall built by a known number of blocks. For the list of numbers, 1 means, place a block in every column. 9 means, place a block every 9 columns. Given a list of numbers and a length, count all the blocks (part 1). Given a known wall, find the list (part 2). Given a known wall segment and a number of blocks, find the length (part 3).
Oh, the circularity! Part 1 uses floor(). For part 2, I can reverse engineer the wall. Is there a block in column 1? Add 1 to the list of numbers and mark all the corresponding blocks. Is there an unmarked block in column 2? Add 2 to the list of numbers and mark blocks. Is there an unmarked block in column 3? Add 3 to the list… For part 3, bisection is good.
..........4..........
......473483436......
....4671465878781....
...219317375373724...
..81639828352872922..
..73694243721961934..
Quest 17. Given a map with numbers and @ marking a volcano, and a rule for how the volcano “grows”, add up all numbers within radius 10 of the volcano (part 1). The volcano grows in steps, find the step with the highest sum of numbers (part 3). Plan a path from S around the volcano and back to S, given the volcano has grown n steps, each step of the path adds the number and the sum mest be less than (n + 1) * 30. Find n.
In part 1, go through the map and remove all the numbers outside the radius, then add up the remaining numbers. In part 2, visit all numbers. Calculate the step, where this number would be affected, and add the number to a corresponding sum. Find the highest sum. In part 3, Dijkstra! This one I had to think about. In part because the path might visit a number twice. But, there’s a way to do it.
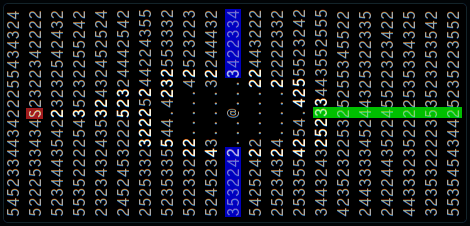
First assume the volcano has grown to radius n. (Beginning with 0.) Then use Dijkstra to find 2 paths, one going clockwise (*) from the red S to a point in the green bar, one counterclockwise. Examine for all points in the green bar. Find the best sum of 2 paths. If it’s too high, calculate the n where this path would have worked, set n to this value and try again. Whew! And I also had to remove my big data structures, when my calculations has finished, or the program would crash.
(*) Force clockwise by removing the lower blue bar.
Plant 1 with thickness 1:
- free branch with thickness 1
Plant 2 with thickness 1:
- free branch with thickness 1
Plant 4 with thickness 17:
- branch to Plant 1 with thickness 15
- branch to Plant 2 with thickness 3
Quest 18. There are plants with branches. Plants like no. 1 can simply be activated. Plants like no. 4 depends on its input from other plants. Given a rule for how plants affect other plants, activate all the simple plants and see how it affects the last plant (part 1). Activate the simple plants using a pattern (part 2). Find the best pattern (part 3).
I had a function to calculate the so called energy for each plant, because I used that code a lot. In part 1 call that function once. In part 2 call it for each pattern. Part 3… For the example data, I could simply try all patterns. But for the notes, a little analysis was required. It turned out, that some simple plants, if activated, would always drag the quality of the pattern down. So, turn on the rest, and boom! Best pattern.
. .......#....#..#........#...#.↑.↑.↑.↑.↑.#.......
9 .......#....#..#...↑....#....↑.↓.↓.↓.↓.↓........
8 ............#..#..↑.↓...#...↑...........↓.......
7 .......↑....#....↑...↓..#..↑............#.......
6 ......↑#↓...#...↑.....↓...↑.............#.......
5 .....↑.#.↓..#..↑.......↓.↑..............#.......
4 ....↑..#..↓.#.↑#........↓...#...........#.......
3 ...↑...#...↓.↑.#............#...........#.......
2 ..↑....#....↓..#............#...........#.......
1 .↑.....#.......#............#...........#.......
↑ S......#.......#........#...#...........#.......
Quest 19. Numbers describe the walls (or rather, the holes in the walls) in a chamber. A rule describes how a duck might fly through the chamber, using the holes. Some of the flight will be flaps upward. Count the flaps (part 1). A wall might have more than 1 hole, find the flight with the lowest number of flaps (part 2 and 3).
There’s recursion involved, because there’s each choice for flap or not flap + the rest of the flight. For small data, trying all choices works fine. For large data… I have a list of the holes. I can calculate the best way to get from a hole to the next. It was fiddly to get this one right. But it’s important to learn. Using sparse data instead of the complete map is a good technique.
T#TTT###T##
.##TT#TT##.
..T###T#T..
...##TT#...
....T##....
.....#.....
Quest 20. A map shows an area with some trampolines. Count pairs of trampolines (part 1). Given 2 points, find the shortest path, jumping between trampolines (part 2). Do it again, but the area is rotating (part 3).
Oh yes. The rotating triangle. But first. Part 1 is very much about interpreting the map correctly. In the top left corner, “T#T” shows a “T#” pair and a “#T” pair. That “#” is also in a pair with a “#” below it, but the “T” on the right is not in a pair with anything below it. Part 2: Convert a Dijkstra to take these pairs into account. Part 3: Implement the rotation. I chose to rotate the jumper. Jump up here, come down there. (Took forever to get right! Better model next time!) And if I come down there, which pairs are available? Wrinkle: I might in essence jump up and down in place. Also, for part 3 I had a more standard graph for Dijkstra. The rotation? Just look at it.
$mn1 = floor($x / 2);
$mn2 = $x % 2;
$m = $mn1 + $mn2;
$n = $mn1;
$op1 = floor($y / 2);
$op2 = $y % 2;
if($mn2 == 0) {
$o = $op1 + $op2;
$p = $op1;
} else {
$p = $op1 + $op2;
$o = $op1;
}
$new_x = $M - 1 - $n + 2 * $o + $p;
$new_y = $M - 1 - $m - $o;
return [$new_x, $new_y];
I’ve done Everybody Codes, back in November.

The Song of Ducks and Dragons [ 2025 ] ![]()
Step 1 [1,2] Step 2 [2,3] Step 3 [3,4] Step 4 [4,5] Step 5 [5,6]
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
*(*) * * * * (*)* * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * * * * * * *
* * * * * * * * * * * * * * *
* * * * * * * * * * * * * * *
* * * * * * * * * *(*)
* * * * * * * * * *
* * * *
Quest 11. Given a list of numbers, interpret them as columns of ducks. A column will check whether the next columns has fewer birds, and if so, move a duck. This happens to all columns. And until no more moves are possible. Then the check goes the other way. The result is a balanced set of columns. Do this for 10 rounds (part 1). Or until balanced (part 2 and 3).
For part 1 and 2, the hardest part was probably to understand what was going on. For part 3… There is a shortcut. I’ve written about why it works. I made a video! Anyway, once the shortcut was in place, it was, again, easy.
989601 989601 989601 989601 989601 989601 989601
857782 857782 857782 857782 857782 857782 857782
746543 746543 746543 746543 746543 746543 746543
766789 766789 766789 766789 766789 766789 766789
Quest 12. Given a map of numbers and a starting point, add numbers to the group of points by adding numbers that are less than or equal to an already added numbers. Do this until no more can be added (part 1). Again with 2 starting points (part 2). Again, with 3 starting points chosen for maximum effect (part 3).
A bit fiddly, but straightforward. In part 3 it turned out to be important, that a good starting point was also a local maximum. If a < b, a can’t set b on fire.
72
58
47
61
67
Quest 13. Given a list of numbers, construct a dial and turn it 2025 times (part 1). Given a list of intervals, construct a dial and turn it 20252025 times (part 2). Again, but 202520252025 times.
In part 3 the numbers got too big. It was important not to construct the whole dial as an array. So, only note beginnings and ends of intervals.
Round 1 Round 2 Round 3 Round 4 Round 5
.#.#.. .###.. #.#.#. #####. ..###.
##.##. #.#### ###.## ...##. ##.###
#.#... #..### #.#.## .#..#. .#.#.#
....## ##...# .#..#. ##.##. .#.###
#.#### #.#.#. #..#.# .####. #...#.
##..#. ...#.. ###.#. .###.# .#...#
Quest 14. A map of tiles. In a game of life way, determine which tiles will be active in the next round. Run some rounds (part 1 and 2). Run a lot of rounds, noting when a certain pattern matches (part 3).
The interesting bit is part 3. Run a few rounds, and keep track of repetitions. Then calculate the rest of the rounds instead of actually going through them. A few interesting questions like how to represent the tiles in a manageable way when recording “I have seen this before”, and then the actual math at the end, trying very hard not to get any off by 1 errors.
start R3 R4 L3
S S### S### S###
# #
# #
# #
# ####
Quest 15. Given a list of instructions about how to walk (turn right and walk 3, turn right again and walk 4…), interpret the walked segments as walls and find the shortest path from start to end (part 1-3).
Dijkstra! And then in part 3, it was necessary to not just build the whole map. Similar to day 13, only build the interesting bits. This was fiddly! A lot of small steps, a lot of testing and correcting errors.
I’ve done Everybody Codes, back in November.

The Song of Ducks and Dragons [ 2025 ] ![]()
AaAaa
AaAaa
AaAaa
AaAaa
AaAaa
Quest 6. Given a list of letters, find all pairs of e.g. “A*a” (part 1 and 2). Repeating the list 1000 times, do it again (part 3).
Part 1 was nice actually. Going through the list, there’s a counter for how many “A”s I’ve seen so far. And when I encounter an “a”, I add that counter value to the running sum. Part 2 was a little more sophisticated, where it had to work without me knowing what letter I was actually looking at. And using ctype_upper() and strtoupper(). Oh, part 3. Here I could use the knowledge, that repeating the list also meant repeating the numbers. With 1000 repetitions, 998 of them are “in the middle”. Count 1 of these and multiply by 998. Then count the 1st and the last. It was a little fiddly. For some reason I didn’t just create my own example data and work on that.
Oronris,Urakris,Oroneth,Uraketh
r > a,i,o
i > p,w
n > e,r
o > n,m
k > f,r
...
Quest 7. Given a list of names and a list of rules, which names follow all the rules (part 1 and 2)? Like, Oronris is out, because s can’t follow i. Then construct all names possible with the rules (part 3).
For part 1 and 2, look at each pair of letters and check whether that exists as a rule. For part 3, oh, recursion. Given part of a name, add all the possible next letters. And check uniqueness, which I didn’t at first!
1,5,2,6,8,4,1,7,3
Quest 8. Given a list of numbers, interpret these as the numbers of nails. So in this list, there’s a string between 1 and 5, between 5 and 2 etc. How many times does a string pass through the center of the circle of nails (part 1)? How many times does a string cross another string (part 2)? Which extra string would cross the most existing strings (part 3)?
The 1st one is easy. Calculate the distance between the 2 nails. If the distance is the same as halfway around the circle, the string will go through the center. In part 2 I use this knowledge: If 2 strings, 1 -> 5 and 7 -> 3, cross each other, it’s because 1 < 3 < 5, but not 1 < 7 < 3. I also have to take care of the edge case, where “both strings use the same nail in 1 end” isn’t counted as crossing. In part 3 I use some of my existing program, but also create all the possible strings. The one I’m looking for might not already exist.
1:CAAGCGCTAAGTTCGCTGGATGTGTGCCCGCG
2:CTTGAATTGGGCCGTTTACCTGGTTTAACCAT
3:CTAGCGCTGAGCTGGCTGCCTGGTTGACCGCG
Quest 9. So called DNA sequences. We have 3 of these, 2 parents and 1 child. For each letter in the sequence, the child should have the same letter as 1 of the parents. Which 1 is the child (part 1 and 2)? Construct a family tree for a lot of people, and measure the largest family (part 3).
Pretty straight forward coding. Can this person be the child of these 2 persons, yes or no? With more than 3 persons, have a 2d array, $children[$parent1][$parent2] = $child. In part 3 I begin by saying all triples are small families. Then I combine these into larger families, until they can’t grow anymore. I got to use “break 3”.
....... ...X... ......D ....... .......
..X.X.. .D..... ....X.. ....... ....X.X
.X...X. ...X... .....X. ....... ...X...
...D... X.X.... ....... ....... .....D.
.X...X. ....... ....... ..X.X.. ...X...
..X.X.. ....... ....... .X...X. ....X.X
....... ....... ....... ...D... .......
Quest 10. Given a map, that’s actually sort of a chessboard, with D marking a dragon moving like a knight, and S marking sheep (no sheep shown above), how many sheep can the dragon reach and eat (part 1)? Add that the sheep can also move and can hide (part 2). Find all games where the dragon eats all the sheep (part 3).
I can see in part 3 I added memoization. And I borrowed code heavily from a colleague. It was hard to keep it straight in my head, where did the dragon go, where did the sheep go, when did a game end with all sheep eaten. On, there’s also recursion.
I’ve done Everybody Codes, back in November. And I got all 60 stars, yeah me! 3 of the stars I only got recently, as among other things Advent of Code and mscroggs arrived in December. Nevertheless!

The Song of Ducks and Dragons [ 2025 ] ![]()
All my code is available ![]() . I aim for low complexity, easily readable code. Including comments. And it’s in PHP.
. I aim for low complexity, easily readable code. Including comments. And it’s in PHP.
Vyrdax
/ \
/ \
Elarzris Drakzyph
\ /
\ /
Fyrryn
Quest 1. Given a list of names, move left and right through the list (part 1). With wrapping (part 2). Or instead of moving around, swap names (part 3).
Create a system to keep track of positions. Use %. Use arrays.
A = [25,9]
R = [ 0,0]
Cycle I
R = R * R = [0,0]
R = R / [10,10] = [0,0]
R = R + A = [25,9]
Quest 2. Given a number, perform a well defined set of math instructions on that number (part 1). Given a map of points, all with coordinates, perform those math instructions of each point (part 2). (Makes a nice picture.) Increase size of map (part 3).
A lot of math. A 2d array.
10,5,1,10,3,8,5,2,2
10 > 8 > 5 > 3 > 2 > 1 the sum of the sizes: 10 + 8 + 5 + 3 + 2 + 1 = 29
10 > 8 > 5 > 2 > 1 the sum of the sizes: 10 + 8 + 5 + 2 + 1 = 26
10 > 5 > 3 > 2 the sum of the sizes: 10 + 5 + 3 + 2 = 20
10 > 5 > 2 the sum of the sizes: 10 + 5 + 2 = 17
Quest 3. Given a list of numbers, create a new list of distinct numbers with the highest sum possible (part 1). Or a list with 20 distinct numbers and the smallest sum possible (part 2). Or the lowest number of lists, covering everything from the original list.
In part 1, simply throw away the duplicates. array_unique(). In part 2, sort the unique numbers and keep the 20 smallest. In part 3, count occurrences of each number and register the largest. array_count_values(). max().
128
64
32
16
8
Quest 4. Interpret a list of numbers as teeth on neighboring gears. If the 1st gear turns 2025 times, how many times does the last gear turn (part 1)? If the last gear turns 10000000000000 times, how many times does the 1st gear turn, rounded up (part 2)? Or do the part 1 calculation again, but with more complicated gears with 2 sets of teeth (part 3).
In part 1 I calculate how many teeth were involved for the 1st gear, and then calculate how many turns that is for the last gear. Part 2 is the same in reverse. In part 3 I did the full calculation, involving all the gears.
3-5-7
|
1-8-10
|
5-9
|
7-8
Quest 5. The fishbone! Given a list of numbers, construct the valid fishbone. Then make other choices based on the result.
As I was basically doing the same thing a lot, I was quick to put stuff into functions. That actually became a guiding principle. If part 2 was “do the same as part 1, but a lot of times”, create a function. A fun function to use was usort(), a custom sorting function. Not very complicated code, just fiddly.
I am also finding a rhythm. I usually build 1 large program, because later parts don’t require a complete rewrite of earlier work. And I get used to the input for the 3 parts being different.