A new December and a new bunch of puzzles from mscroggs.co.uk.
Here we are helped by a very nice pattern for 15n.
Very quickly for odd n, the last 3 digits are 375, and for even n, the last 3 digits are 625. The n in the question is even, so the answer is 625.
This December I participated in Advent of Code.
Ah yes. It took me a little while to wrap my head around “2 equations with 2 variables”. Doh. And then it took me a little while to actually implement a standard solution. (Question.) Double doh.
For part 2 I had to change 2 lines, so below is only part 2.
Part 2:
<?php
$input = file_get_contents('./d13input2.txt', true);
$rules = array();
$i = 0;
foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
if(preg_match("/Button A/",$line,$matches)) {
if(preg_match_all("/(\d+)/",$line,$matches)) {
$rules[$i]["ax"] = $matches[0][0];
$rules[$i]["ay"] = $matches[0][1];
}
}
if(preg_match("/Button B/",$line,$matches)) {
if(preg_match_all("/(\d+)/",$line,$matches)) {
$rules[$i]["bx"] = $matches[0][0];
$rules[$i]["by"] = $matches[0][1];
}
}
if(preg_match("/Prize/",$line,$matches)) {
if(preg_match_all("/(\d+)/",$line,$matches)) {
// part 1 doesn't have the +10000000000000
$rules[$i]["px"] = $matches[0][0] + 10000000000000;
$rules[$i]["py"] = $matches[0][1] + 10000000000000;
}
}
if(strlen($line) < 2) {
$i++;
}
}
$money = 0;
$hits = 0;
foreach($rules as $rule) {
// Coefficients of the equations
$a1 = $rule["ax"]; $b1 = $rule["bx"]; $c1 = $rule["px"];
$a2 = $rule["ay"]; $b2 = $rule["by"]; $c2 = $rule["py"];
// Calculate the determinant
$determinant = $a1 * $b2 - $a2 * $b1;
if ($determinant == 0) {
// The system has no unique solution
// (either no solution or infinitely many solutions)
} else {
// Calculate x and y using Cramer's Rule
$x = ($c1 * $b2 - $c2 * $b1) / $determinant;
$y = ($a1 * $c2 - $a2 * $c1) / $determinant;
}
$soln = $y;
$solm = $x;
if(abs((int)$soln - $soln) < 0.01
&& abs((int)$solm - $solm) < 0.01) {
if($solm > 0 && $soln > 0) {
$money += $solm * 3 + $soln;
$hits++;
}
}
}
print("$hits $money\n");
?>A new December and a new bunch of puzzles from mscroggs.co.uk.
Let the square be:
abc def ghi
Rules:
From these we can deduce these further rules:
Assume i = 0. Then by (1) f = 0. Then by (4) h = 0. Then by (1) e = 0. But by (3), then b = 19, not a digit. So, i != 0.
i = 5. Then by (1) f = 0. Then by (4), c05 = 3 gh5, this might be 405 = 3 * 135 or 705 = 3 * 235. In both cases h = 3. g might be 1 or 2. c might be 4 or 7. Then by (1) e = 7. Then by (3) b = 9.
So far we have:
a9c d70 g35
Assume g = 1. Then by (1) d = 2. Then by (2) a = 12, not a digit. So, g != 1.
g = 2. Then by (1) d = 4. Then by (2) a = 9. Then by (4) c = 7.
The sought after number, abc, is 997.
This December I participated in Advent of Code.
This one had me thinking.
Part 1:
<?php
$input = file_get_contents('./d12input1.txt', true);
foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
if(strlen($line)>2) {
$map[] = str_split($line);
}
}
$mapx = sizeof($map);
$mapy = sizeof($map[0]);
// name possible areas
$names = array();
for($i=0;$i<sizeof($map);$i++) {
for($j=0;$j<sizeof($map[$i]);$j++) {
$names[$map[$i][$j]] = 1;
}
}
// convert names
$names2 = array();
foreach($names as $key => $val) {
$names2[] = $key;
}
$names = $names2;
// thin areas out
$areas = array();
for($k=0;$k<sizeof($names);$k++) {
$lett = $names[$k];
$tmp = $map;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if($tmp[$i][$j] != $lett) {
unset($tmp[$i][$j]);
}
}
}
$areas[$k] = $tmp;
}
function subtst($i, $j) {
global $tmpb;
//print_r($tmpb);
if(isset($tmpb[$i-1][$j])) {
if($tmpb[$i-1][$j] != "*") {
$tmpb[$i-1][$j] = "*";
subtst($i-1, $j);
}
}
if(isset($tmpb[$i+1][$j])) {
if($tmpb[$i+1][$j] != "*") {
$tmpb[$i+1][$j] = "*";
subtst($i+1, $j);
}
}
if(isset($tmpb[$i][$j-1])) {
if($tmpb[$i][$j-1] != "*") {
$tmpb[$i][$j-1] = "*";
subtst($i, $j-1);
}
}
if(isset($tmpb[$i][$j+1])) {
if($tmpb[$i][$j+1] != "*") {
$tmpb[$i][$j+1] = "*";
subtst($i, $j+1);
}
}
}
function atst() {
global $tmp, $map, $tmpb, $key, $mapx, $mapy, $areas;
// grab random beginning point
$lett = "";
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($tmp[$i][$j])) {
$lett = $tmp[$i][$j];
$x = $i;
$y = $j;
break 2;
}
}
}
// can I reach all points from here?
$tmpb = $tmp;
$tmpb[$x][$y] = "*";
subtst($x, $y);
if(sizeof(array_count_values(array_merge(...$tmpb))) > 1) {
$new1 = $tmpb;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($new1[$i][$j])) {
if($new1[$i][$j] == $lett) {
unset($new1[$i][$j]);
} else {
$new1[$i][$j] = $lett;
}
}
}
}
$new2 = $tmpb;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($new2[$i][$j])) {
if($new2[$i][$j] != $lett) {
unset($new2[$i][$j]);
}
}
}
}
$areas[$key] = $new1;
$areas[] = $new2;
}
}
// if areas aren't actually connected, split up
$areaz = 0;
while($areaz < sizeof($areas)) {
$areaz = sizeof($areas);
foreach($areas as $key => $area) {
$tmp = $area;
atst();
}
}
$sum = 0;
foreach($areas as $key => $area) {
$sz1 = array_count_values(array_merge(...$area));
$sz2 = array_pop($sz1);
$per = 0;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($area[$i][$j])) {
if(!isset($area[$i-1][$j])) {
$per++;
}
if(!isset($area[$i+1][$j])) {
$per++;
}
if(!isset($area[$i][$j-1])) {
$per++;
}
if(!isset($area[$i][$j+1])) {
$per++;
}
}
}
}
$sum += $sz2 * $per;
}
print("$sum\n");
?>Part 2:
<?php
$input = file_get_contents('./d12input2.txt', true);
foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
if(strlen($line)>2) {
$map[] = str_split($line);
}
}
$mapx = sizeof($map);
$mapy = sizeof($map[0]);
// name possible areas
$names = array();
for($i=0;$i<sizeof($map);$i++) {
for($j=0;$j<sizeof($map[$i]);$j++) {
$names[$map[$i][$j]] = 1;
}
}
// convert names
$names2 = array();
foreach($names as $key => $val) {
$names2[] = $key;
}
$names = $names2;
// thin areas out
$areas = array();
for($k=0;$k<sizeof($names);$k++) {
$lett = $names[$k];
$tmp = $map;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if($tmp[$i][$j] != $lett) {
unset($tmp[$i][$j]);
}
}
}
$areas[$k] = $tmp;
}
//print_r($areas);
function subtst($i, $j) {
global $tmpb;
if(isset($tmpb[$i-1][$j])) {
if($tmpb[$i-1][$j] != "*") {
$tmpb[$i-1][$j] = "*";
subtst($i-1, $j);
}
}
if(isset($tmpb[$i+1][$j])) {
if($tmpb[$i+1][$j] != "*") {
$tmpb[$i+1][$j] = "*";
subtst($i+1, $j);
}
}
if(isset($tmpb[$i][$j-1])) {
if($tmpb[$i][$j-1] != "*") {
$tmpb[$i][$j-1] = "*";
subtst($i, $j-1);
}
}
if(isset($tmpb[$i][$j+1])) {
if($tmpb[$i][$j+1] != "*") {
$tmpb[$i][$j+1] = "*";
subtst($i, $j+1);
}
}
}
function atst() {
global $tmp, $map, $tmpb, $key, $mapx, $mapy, $areas;
// grab random beginning point
$lett = "";
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($tmp[$i][$j])) {
$lett = $tmp[$i][$j];
$x = $i;
$y = $j;
break 2;
}
}
}
// can I reach all points from here?
$tmpb = $tmp;
$tmpb[$x][$y] = "*";
subtst($x, $y);
if(sizeof(array_count_values(array_merge(...$tmpb))) > 1) {
//print("alert\n");
$new1 = $tmpb;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($new1[$i][$j])) {
if($new1[$i][$j] == $lett) {
unset($new1[$i][$j]);
} else {
$new1[$i][$j] = $lett;
}
}
}
}
$new2 = $tmpb;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($new2[$i][$j])) {
if($new2[$i][$j] != $lett) {
unset($new2[$i][$j]);
}
}
}
}
$areas[$key] = $new1;
$areas[] = $new2;
}
}
// if areas aren't actually connected, split up
$areaz = 0;
while($areaz < sizeof($areas)) {
$areaz = sizeof($areas);
foreach($areas as $key => $area) {
$tmp = $area;
atst();
}
}
$sum = 0;
foreach($areas as $key => $area) {
$sz1 = array_count_values(array_merge(...$area));
$sz2 = array_pop($sz1);
$per = 0;
for($i=0;$i<$mapx;$i++) {
for($j=0;$j<$mapy;$j++) {
if(isset($area[$i][$j])) {
// above
if(!isset($area[$i-1][$j])) {
// already counted?
if(isset($area[$i][$j-1]) && !isset($area[$i-1][$j-1])) {
} else {
$per++;
}
}
// below
if(!isset($area[$i+1][$j])) {
// already counted?
if(isset($area[$i][$j-1]) && !isset($area[$i+1][$j-1])) {
} else {
$per++;
}
}
// to the left
if(!isset($area[$i][$j-1])) {
// already counted?
if(isset($area[$i-1][$j]) && !isset($area[$i-1][$j-1])) {
} else {
$per++;
}
}
// to the right
if(!isset($area[$i][$j+1])) {
// already counted?
if(isset($area[$i-1][$j]) && !isset($area[$i-1][$j+1])) {
} else {
$per++;
}
}
}
}
}
$sum += $sz2 * $per;
}
print("$sum\n");
?>A new December and a new bunch of puzzles from mscroggs.co.uk.
Holly picks the 3-digit number abc. Then she removes either a, b or c to get a new 2-digit number. Adding these 2 numbers together gets 309. 309 is odd, therefore removing a digit from abc can’t preserve c as the last digit, as that would make the sum even. So we have:
309 = abc + ab
If b + a = 0, a = 3 is impossible.
Therefore a = 2, b = 8, c = 1. So abc = 281.
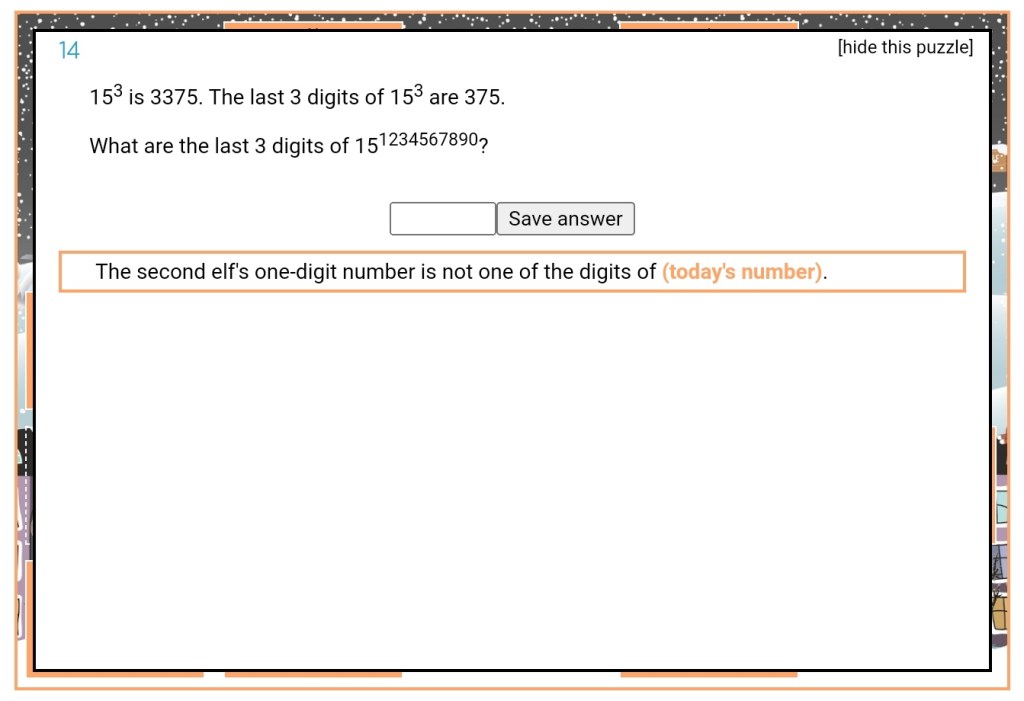
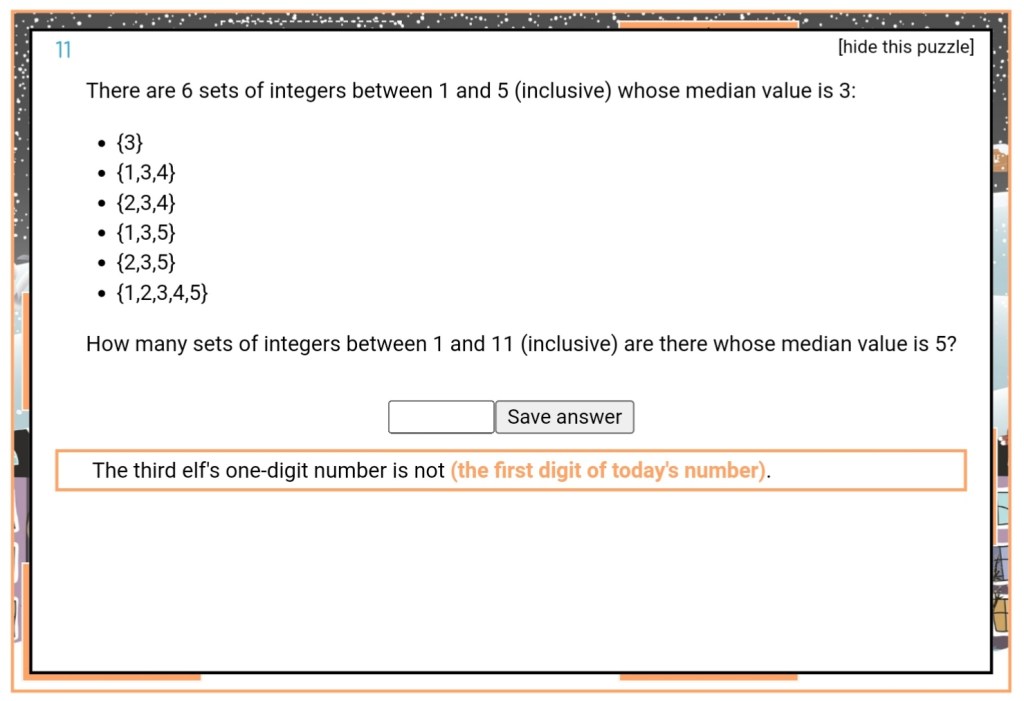
This December I participated in Advent of Code.
This is a case of, part 1 can be brute forced, part 2 can’t. Part 1 is straightforward. Simply keep a list of the numbers from each step. In part 2 it matters, that the order doesn’t matter. If I may say so. Instead of keeping a list of the numbers, I keep a count. How many 0s, how many 1s etc. So e.g. in a step I say, I previously had x 0s, now I have x 1s. I previously had y 1s, now I have y 2024s. I previously had z 2024s, now I have z 20s and z 24s. Etc. Adding everything up, because there might be more than one source for the numbers in the next step.
I liked this one!
Part 1:
<?php
$input = file_get_contents('./d11input2.txt', true);
foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
if(strlen($line)>2) {
$num1 = explode(" ", $line);
}
}
/*
If the stone is engraved with the number 0, it is replaced by a stone engraved with the number 1.
If the stone is engraved with a number that has an even number of digits, it is replaced by two stones. The left half of the digits are engraved on the new left stone, and the right half of the digits are engraved on the new right stone. (The new numbers don't keep extra leading zeroes: 1000 would become stones 10 and 0.)
If none of the other rules apply, the stone is replaced by a new stone; the old stone's number multiplied by 2024 is engraved on the new stone.
*/
for($i=0;$i<25;$i++) {
for($j=0;$j<sizeof($num1);$j++) {
$num = $num1[$j];
if($num == 0) {
$num2[] = 1;
continue;
}
$numl = strlen((string) $num);
if($numl % 2 == 0) {
$num2[] = (int) substr((string) $num, 0, $numl/2);
$num2[] = (int) substr((string) $num, $numl/2, $numl/2);
continue;
}
$num2[] = $num * 2024;
}
$num1 = $num2;
$num2 = array();
}
print(sizeof($num1)."\n");
?>Part 2:
<?php
$input = file_get_contents('./d11input2.txt', true);
foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
if(strlen($line)>2) {
$num1 = explode(" ", $line);
}
}
for($j=0;$j<sizeof($num1);$j++) {
$num = $num1[$j];
if(isset($num2[$num])) {
$num2[$num]++;
} else {
$num2[$num] = 1;
}
}
$num1 = $num2;
$num2 = array();
/*
If the stone is engraved with the number 0, it is replaced by a stone engraved with the number 1.
If the stone is engraved with a number that has an even number of digits, it is replaced by two stones. The left half of the digits are engraved on the new left stone, and the right half of the digits are engraved on the new right stone. (The new numbers don't keep extra leading zeroes: 1000 would become stones 10 and 0.)
If none of the other rules apply, the stone is replaced by a new stone; the old stone's number multiplied by 2024 is engraved on the new stone.
*/
for($i=0;$i<75;$i++) {
foreach($num1 as $num => $nom) {
if($num == 0) {
if(isset($num2[1])) {
$num2[1] += $nom;
} else {
$num2[1] = $nom;
}
continue;
}
$numl = strlen((string) $num);
if($numl % 2 == 0) {
$numa = (int) substr((string) $num, 0, $numl/2);
if(isset($num2[$numa])) {
$num2[$numa] += $nom;
} else {
$num2[$numa] = $nom;
}
$numb = (int) substr((string) $num, $numl/2, $numl/2);
if(isset($num2[$numb])) {
$num2[$numb] += $nom;
} else {
$num2[$numb] = $nom;
}
continue;
}
$numc = $num * 2024;
if(isset($num2[$numc])) {
$num2[$numc] += $nom;
} else {
$num2[$numc] = $nom;
}
}
$num1 = $num2;
$num2 = array();
}
print(array_sum($num1)."\n");
?>A new December and a new bunch of puzzles from mscroggs.co.uk.
Out of the 11 available integers, 5 is the 5th, with 4 integers before it and 6 after. A set of integers is well formed, if 5 is the middle integer, with n integers before it and n after.
n = 0, 1 way to do that.
n = 1, 4 choices in front, 6 choices after, 4*6 = 24 ways to do that.
n = 2, (4 c 2) choices in front, (6 c 2) choices after, (4 c 2) * (6 c 2) = 4*3/2 * 6*5/2 = 6*15 = 90 ways to do that.
n = 3, (4 c 3) choices in front, (6 c 3) choices after, (4 c 3) * (6 * 3) = 4 * 6*5*4/(3*2) = 4*20 = 80 ways to do that.
n = 4, 1 choice in front, (6 c 4) choices after, 6*5/2 = 15 ways to do that.
1+24+90+80+15 = 210.
This December I participated in Advent of Code.
Days 7-10 saw me really trying (most days) to get a good ranking. (A good ranking turned out to be “a 4 digit number”.) I would be ready when the new puzzle dropped, sitting at my PC. And I would get the programming done! This later flagged, when the puzzles got harder, and I had to spend time simply trying to figure out what coding to do. But in this period, it was very much possible to get a good ranking. (From day 16 and forward, I was trying to catch up. It was a struggle to get the program done within 24 hours, and I wanted to solve the puzzles in the right order.)
--------Part 1-------- --------Part 2--------
Day Time Rank Score Time Rank Score
25 >24h 22113 0 >24h 14148 0
24 >24h 23368 0 >24h 15862 0
23 >24h 23812 0 >24h 21472 0
22 >24h 25204 0 >24h 21799 0
21 >24h 19594 0 >24h 16355 0
20 >24h 24815 0 >24h 21577 0
19 >24h 28005 0 >24h 25333 0
18 >24h 27991 0 >24h 27338 0
17 >24h 28700 0 >24h 20591 0
16 >24h 24090 0 >24h 25303 0
15 01:19:07 5843 0 07:18:20 8861 0
14 01:28:12 7258 0 02:13:42 6000 0
13 03:04:50 11545 0 03:08:52 7714 0
12 03:55:52 14298 0 04:04:26 7259 0
11 00:24:58 6479 0 01:09:10 5330 0
10 00:44:34 6515 0 00:48:19 6013 0
9 01:26:25 9059 0 02:59:32 8039 0
8 01:53:25 10087 0 02:04:40 9294 0
7 17:55:39 47349 0 18:02:03 44377 0
6 00:45:55 8375 0 02:18:28 8078 0
5 13:07:46 55110 0 13:13:45 44839 0
4 01:51:36 15622 0 02:06:52 13570 0
3 16:51:27 91593 0 17:04:46 80436 0
2 12:11:26 78108 0 13:30:49 60978 0
1 17:12:43 92846 0 17:24:33 87414 0
Day 9 I had a question. The answer turned out to be: I had a check in part 1, that I lost when I restructured the code for part 2. Oops.
Day 7: wonderful recursion! Day 10: more wonderful recursion!
A new December and a new bunch of puzzles from mscroggs.co.uk.
The candidate numbers all have 2 digits, ab. A palindrome number of this kind has a = b. So the palindrome numbers are 11, 22, …, 99.
11 + 22 + … + 99 =
(1+2+…+9)*11 =
9*5*11 =
495
A new December and a new bunch of puzzles from mscroggs.co.uk.
Oh goody, time to use my fairly new cross sum skills.
Going left to right, top to bottom, name the boxes a-i.
(*) Row 2, column 3.
The digits in the boxes are 7, 9 and 4. 7*9*4 = 252.
Stuff from ommadawn.dk (Lise Andreasen) 