This December I participated in Advent of Code.

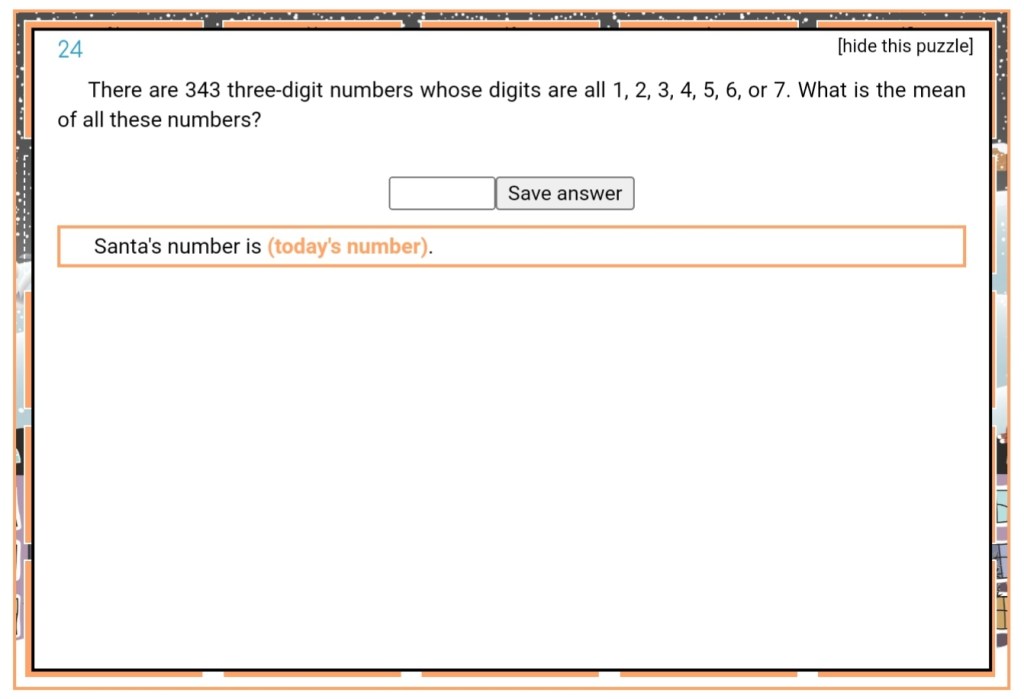
So. Looking back. Days 1-10 were fun, because it was fun to code again. Day 16 (1 point for walking forwards, 1000 to turn) was fun, after the fact, because I found an elegant way (with a nice diagram) to represent the labyrinth as a graph, and finally just implemented Dijkstra fully. Day 17 (build a small programming language) was very satisfying to solve, even if it involved a lot of paper. For day 19 (towels) I had to learn memoization. (I never learned this before?) Day 20 (a labyrinth that turns out just to be one long path, and it’s possible to walk through walls) it was an epiphany, that (part 1 of route) + (part 2 of route) – (discarded part in the middle) + (shortcut) was a way to solve the puzzle. Day 24 (a lot of gates) required some paperwork.

This is my attempt to fill out the complete personal times for me. I’m a little sad, that it simply says “more than 24 hours” officially.

Part 1 of days 17, 22 and 23 must have been easy, I spent minutes getting them right (just 2 or 7 or 8 days late). As I remember it, day 25 didn’t take a long time either, but I wanted to be well rested before I attempted it, so, happy surprise.

      --------Part 1--------   --------Part 2--------
Day       Time   Rank  Score       Time   Rank  Score
 25 8:03:01     22113      0 8:03:02     14148      0
 24 7:10:58     23368      0 8:11:00     15862      0
 23 7:20:30     23812      0 8:10:15     21472      0
 22 8:17:59     25204      0 8:20:00     21799      0
 21 9:10:07     19594      0 9:17:22     16355      0
 20 5:05:00     24815      0 6:02:28     21577      0
 19 4:06:00     28005      0 4:08:12     25333      0
 18 4:11:11     27991      0 4:11:49     27338      0
 17 2:09:34     28700      0 3:08:04     20591      0
 16 2:06:05     24090      0 3:08:50     25303      0
 15   01:19:07   5843      0   07:18:20   8861      0
 14   01:28:12   7258      0   02:13:42   6000      0
 13   03:04:50  11545      0   03:08:52   7714      0
 12   03:55:52  14298      0   04:04:26   7259      0
 11   00:24:58   6479      0   01:09:10   5330      0
 10   00:44:34   6515      0   00:48:19   6013      0
  9   01:26:25   9059      0   02:59:32   8039      0
  8   01:53:25  10087      0   02:04:40   9294      0
  7   17:55:39  47349      0   18:02:03  44377      0
  6   00:45:55   8375      0   02:18:28   8078      0
  5   13:07:46  55110      0   13:13:45  44839      0
  4   01:51:36  15622      0   02:06:52  13570      0
  3   16:51:27  91593      0   17:04:46  80436      0
  2   12:11:26  78108      0   13:30:49  60978      0
  1   17:12:43  92846      0   17:24:33  87414      0

This is, for completeness, based on these timestamps:

-rw-rw-r-- 1 slimbook slimbook      6773 Dec 19 14:50 d16c.php
-rw-rw-r-- 1 slimbook slimbook      4921 Dec 19 15:34 d17a.php
-rw-rw-r-- 1 slimbook slimbook     93787 Dec 20 14:04 day17b.ods
-rw-rw-r-- 1 slimbook slimbook      6166 Dec 22 17:11 d18a.php
-rw-rw-r-- 1 slimbook slimbook      6679 Dec 22 17:49 d18b.php
-rw-rw-r-- 1 slimbook slimbook      2092 Dec 23 08:43 d19a.php not right!!!
                                                12:00 ?
-rw-rw-r-- 1 slimbook slimbook      1075 Dec 23 16:12 d19b.php
-rw-rw-r-- 1 slimbook slimbook      4482 Dec 25 11:00 d20b.php
-rw-rw-r-- 1 slimbook slimbook      4393 Dec 26 08:28 d20c.php
-rw-rw-r-- 1 slimbook slimbook      9763 Dec 30 16:07 d21c.php
-rw-rw-r-- 1 slimbook slimbook     10164 Dec 30 23:22 d21e.php
-rw-rw-r-- 1 slimbook slimbook      1371 Dec 30 23:59 d22a.php
-rw-rw-r-- 1 slimbook slimbook      1951 Dec 31 02:00 d22b.php
-rw-rw-r-- 1 slimbook slimbook      1645 Dec 31 02:30 d23a.php
-rw-rw-r-- 1 slimbook slimbook       783 Dec 31 16:15 d23tmp.txt

-rw-rw-r-- 1 slimbook slimbook      1878 Dec 31 16:58 d24a.php
-rw-rw-r-- 1 slimbook slimbook      7940 Jan  1 17:00 d24mermaid3.txt
-rw-rw-r-- 1 slimbook slimbook      1217 Jan  2 09:01 d25a.php
                                                09:02

This December I participated in Advent of Code.

Part 1 was sort of easy. Check whether a lock pin and key pin overlap in this particular combination, and go through all the possible combinations, counting. Part 2 turned out to be: Complete all the 49 other parts this December, and click this link!

Part 1:

<?php

///////////////////////////////////////////////////

$input = file_get_contents('./d25input2.txt', true);

$item = 0;
foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
  if(strlen($line)>2) {
    $items[$item][] = str_split($line);
  } else {
    $item++;
  }
}

foreach($items as $item) {
  $tmp = implode($item[0]);
  if($tmp == "#####") {
    $locks[] = $item;
  } else {
    $keys[] = $item;
  }
}

foreach($locks as $id => $lock) {
  // each pin, 5 of them
  for($i=0;$i<5;$i++) {
    // each pin element, 7 of them
    $pinh = 0;
    for($j=1;$j<7;$j++) {
      if($lock[$j][$i] == "#") {
        $pinh++;
      }
    }
    $locksig[$id][] = $pinh;
  }
}

foreach($keys as $id => $key) {
  // each pin, 5 of them
  for($i=0;$i<5;$i++) {
    // each pin element, 7 of them
    $pinh = 0;
    for($j=5;$j>0;$j--) {
      if($key[$j][$i] == "#") {
        $pinh++;
      }
    }
    $keysig[$id][] = $pinh;
  }
}

$lockkeymatch = 0;

foreach($locksig as $lock) {
  foreach($keysig as $key) {
    $tmp = array();
    for($i=0;$i<5;$i++) {
      $tmp[] = $lock[$i] + $key[$i];
    }
    if(max($tmp) <= 5) {
      $lockkeymatch++;
    }
  }
}

print("$lockkeymatch\n");

?>

A new December and a new bunch of puzzles from mscroggs.co.uk.

All the hints:

Day	Clue
1	144 is an elf’s three-digit number.
2	The first elf’s one-digit number is not a factor of 202.
3	The first elf’s one-digit number is not 7.
4	The third elf’s one-digit number is not 9.
5	The second elf’s one-digit number is not 1, 7, or 9.
6	990 is a multiple of an elf’s three-digit number.
7	The third elf’s one-digit number is not 1.
8	The third elf’s one-digit number is not a factor of 432.
9	The first elf’s one-digit number is not 5.
10	The second elf’s one-digit number is not 4, 9, or 5.
11	The third elf’s one-digit number is not 2.
12	The second elf’s one-digit number is not 2, 8, or 1.
13	One of the digits of the second elf’s three-digit number is 9.
14	The second elf’s one-digit number is not 6, 2, or 5.
15	The third elf’s one-digit number is not 7.
16	The first elf’s one-digit number is not 3.
17	The first elf’s one-digit number is not 9.
18	The first elf’s one-digit number is not 6.
19	The highest common factor of 256 and the second elf’s three-digit number is 1.
20	The third elf’s one-digit number is not 4.
21	138 is an elf’s three-digit number.
22	The highest common factor of 851 and the third elf’s three-digit number is 1.
23	The highest common factor of the first and third elves’ one-digit numbers is not 2, 4, or 1.
24	Santa’s number is 444.

And I know no. 8 and 23 are wrong.

My first look at this problem:

• (aaa – bbb)*c = x
• (x – ddd)*e = y
• (y – fff)*g = hhhhh

Let’s sort this a little bit.

Day	Clue
24	Santa’s number is 444.

Very clear, and as I suspected, very late in the game. aaa = 444.

Day	Clue
1	144 is an elf’s three-digit number.
6	990 is a multiple of an elf’s three-digit number.
13	One of the digits of the second elf’s three-digit number is 9.
19	The highest common factor of 256 and the second elf’s three-digit number is 1.
21	138 is an elf’s three-digit number.
22	The highest common factor of 851 and the third elf’s three-digit number is 1.

Or to put it another way:

• We’re looking for bbb, ddd and fff.
• One of these is 144.
• One of these is 138. (6 * 23)
• One of these is a multiple of 990, therefore one of these: 110, 165, 198, 330, 495, 990. There’s no overlap with the 2 we already have, so this must be the third one.
• One of the digits of ddd is 9. This must be the “multiple of 990” one.
• As 256 is 2⁸, ddd must be odd.
• Combining these 3 facts, we get ddd = 495.
• As 851 = 23 * 37, fff can’t be 138. fff = 144.
• bbb = 138.

Day	Clue
2	The first elf’s one-digit number is not a factor of 202.
3	The first elf’s one-digit number is not 7.
9	The first elf’s one-digit number is not 5.
16	The first elf’s one-digit number is not 3.
17	The first elf’s one-digit number is not 9.
18	The first elf’s one-digit number is not 6.

c can’t be 2, 7, 5, 3, 9 or 6. This leaves 1, 4 and 8. (I assume for now, that none of the 1 digit numbers are 0.)

Day	Clue
5	The second elf’s one-digit number is not 1, 7, or 9.
10	The second elf’s one-digit number is not 4, 9, or 5.
12	The second elf’s one-digit number is not 2, 8, or 1.
14	The second elf’s one-digit number is not 6, 2, or 5.

e can’t be 1, 7, 9, 4, 5, 2, 8, 6. This leaves 3.

Day	Clue
4	The third elf’s one-digit number is not 9.
7	The third elf’s one-digit number is not 1.
11	The third elf’s one-digit number is not 2.
15	The third elf’s one-digit number is not 7.
20	The third elf’s one-digit number is not 4.

g can’t be 9, 1, 2, 7 or 4. This leaves 3, 5, 6 and 8.

Let’s repeat that:

• (aaa – bbb)*c = x
• (x – ddd)*e = y
• (y – fff)*g = hhhhh
• aaa = 444
• bbb = 138
• c is 1, 4 or 8
• ddd = 495
• e = 3
• fff = 144
• g is 3, 5, 6 or 8

Now it’s just a question of going through all the options. Discarding the negative options for hhhhh first, and testing the true 5 digit options next.

444	138	1	495	3	144	3	-2133
444	138	4	495	3	144	3	6129
444	138	8	495	3	144	3	17145	no
444	138	1	495	3	144	5	-3555
444	138	4	495	3	144	5	10215	no
444	138	8	495	3	144	5	28575	no
444	138	1	495	3	144	6	-4266
444	138	4	495	3	144	6	12258
444	138	8	495	3	144	6	34290	no
444	138	1	495	3	144	8	-5688
444	138	4	495	3	144	8	16344	ja
444	138	8	495	3	144	8	45720	no

Hey! Turns out, (((444-138)*4-495)*3-144)*8 = 16344.

This December I participated in Advent of Code.

One of those days, where I probably grumbled a lot. Part 1 was easy. I chose an algorithm, where I went through a list of all the expressions, checked whether the gate’s output could be calculated (and if yes, deleted the expression from the list), looped back and did it again, until the list was empty. Part 2… I tried several different approaches. Reading hints from others, I ultimately used a free online diagram tool, Mermaid, that accepts text input. Perfect. I wrote a small program to turn the input into something Mermaid could understand (every value, value, gate, value, turned into 2 x value, arrow, value). Then I tried to analyze this diagram. Printed a lot of full adders. And began copying the diagram on to these. Every time the diagram wouldn’t fit, I’d found a swap. Then it took some thinking to figure out how to swap back. But I got there!

Part 1:

<?php

///////////////////////////////////////

$input = file_get_contents('./d24input2.txt', true);

foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
  if(strlen($line)>2) {
    // x00: 1
    if(preg_match("/^(\w+): (\d)$/", $line, $m)) {
      $values[$m[1]] = $m[2];
    }
    // ntg XOR fgs -> mjb
    if(preg_match("/->/", $line, $m)) {
      $m = explode(" ", $line);
      $expr[] = $m;
    }
  }
}

while(sizeof($expr) > 0) {
  foreach($expr as $key => $exp) {
    $val1 = $exp[0];
    $val2 = $exp[2];
    if(isset($values[$val1]) && isset($values[$val2])) {
      $gate = $exp[1];
      $val3 = $exp[4];
      switch($gate) {
        case "AND":
          $values[$val3] =
            $values[$val1] * $values[$val2];
          break;
        case "OR":
          $values[$val3] =
            $values[$val1] + $values[$val2] 
            - $values[$val1] * $values[$val2];
          break;
        case "XOR":
          $values[$val3] =
            ($values[$val1] + $values[$val2]) % 2;
          break;
      }
      unset($expr[$key]);
    }
  }
}

$allzs = $values;
foreach($allzs as $key => $posz) {
  if(!preg_match("/z/", $key, $m)) {
    unset($allzs[$key]);
  }
}

print_r($allzs);

$sum = 0;
foreach($allzs as $key => $z) {
  $pos = (int) str_replace("z", "", $key);
  $sum += $z * pow(2, $pos);
}

print("$sum\n");
?>

Part 2:

Big diagram. Small diagrams.

A new December and a new bunch of puzzles from mscroggs.co.uk.

All the possible 3 digit numbers are here. E.g. we have 111, 211, 311, 411, 511, 611 and 711. For these the mean of the first digit is 4. Expanding this to all the possibilities, the mean for every digit is 4. The result is 444.

This December I participated in Advent of Code.

For part 1, I optimized a little. Like only storing the representation of each 3 way computer group once. Also 3d arrays. For part 2… I flirted a little with BK (ehm, can’t remember what that stands for), but that program seemed to never stop. So I did it differently. Just like part 1 asked me to create all the 3 way groups, I now moved on to create all the 4 way groups, 5 way groups etc. As each computer had about 13 friends, this shouldn’t take forever to get through. I think it took 35 minutes. I stopped when I only had 1 group of the current size. Oh yeah, and I changed the data structure a little. (BK was sort of the other way around. Trying to grow 1 large set greedily.)

Part 1:

<?php

//////////////////////////////////

$input = file_get_contents('./d23input2.txt', true);

foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
  if(strlen($line)>2) {
    $conn1[] = explode("-", $line);
  }
}

foreach($conn1 as $comp) {
  $comp1 = $comp[0];
  $comp2 = $comp[1];
  $conn2[$comp1][$comp2] = 1;
  $conn2[$comp2][$comp1] = 1;
}

foreach($conn2 as $comp1 => $c1con) {
  foreach($c1con as $comp2 => $cona) {
    foreach($c1con as $comp3 => $conb) {
      // make sure comp2 and comp3 are different
      if(isset($conn2[$comp2][$comp3])) {
        // only store the 3 way connection alphabetically, so as not to store it 6 times
        if(strcmp($comp1,$comp2) < 0 && strcmp($comp2,$comp3) < 0) {
          // only store this set, if one of the computers begin with t
          if(substr($comp1, 0, 1) == "t" || substr($comp2, 0, 1) == "t" || substr($comp3, 0, 1) == "t") {
            $conn3[$comp1][$comp2][$comp3] = 1;
          }
        }
      }
    }
  }
}

$sum = 0;
foreach($conn3 as $a) {
  foreach($a as $b) {
    foreach($b as $c) {
      $sum += $c;
    }
  }
}
print("$sum\n");

?>

Part 2:

<?php

//////////////////////////////////

$input = file_get_contents('./d23input1.txt', true);

foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
  if(strlen($line)>2) {
    $conn1[] = explode("-", $line);
  }
}

foreach($conn1 as $comp) {
  $comp1 = $comp[0];
  $comp2 = $comp[1];
  $conn2[$comp1][$comp2] = 1;
  $conn2[$comp2][$comp1] = 1;
}

foreach($conn2 as $comp1 => $c1con) {
  foreach($c1con as $comp2 => $cona) {
    foreach($c1con as $comp3 => $conb) {
      // make sure comp2 and comp3 are different
      if(isset($conn2[$comp2][$comp3])) {
        // only store the 3 way connection alphabetically, so as not to store it 6 times
        if(strcmp($comp1,$comp2) < 0 && strcmp($comp2,$comp3) < 0) {
          //$conn3[$comp1][$comp2][$comp3] = 1;
          $conn3b[] = array($comp1, $comp2, $comp3);
        }
      }
    }
  }
}

$allcomp = array_keys($conn2);

$multiple = sizeof($conn3b);
$connx = $conn3b;
while($multiple > 1) {
  print("No. of sets in the iteration: $multiple\n");
  $conny = array();
  // build new arrays of length y from length x - y = x+1
  foreach($connx as $wayx) {
    foreach($allcomp as $key => $newcomp) {
      // test that computer is not already in array
      if(!in_array($newcomp, $wayx)) {
        $newgood = 1;
        // test that new is connected to all in wayx
        foreach($wayx as $oldcomp) {
          if(!isset($conn2[$oldcomp][$newcomp])) {
            $newgood = 0;
            break;
          }
        }
        if($newgood == 1) {
          // create new wayy
          $wayytmp = $wayx;
          array_push($wayytmp, $newcomp);
          sort($wayytmp);
          if(!in_array($wayytmp, $conny)) {
            $conny[] = $wayytmp;
          }
        }
      }
    }
  }
  
  $multiple = sizeof($conny);
  if($multiple == 1) {
    print("Max set found!\n");
    print_r($conny);
  }
  $connx = $conny;
}

?>

A new December and a new bunch of puzzles from mscroggs.co.uk.

I don’t really have any ideas for solving this. There’s an official solution at the site by now.

This December I participated in Advent of Code.

For this one, it actually took me a long time to understand the instructions. Hence a big comment in the important function. Once that was established, part 1 was sort of easy. For part 2… Oh, wonderful 5d arrays! I had to calculate the price for each sequence, for each buyer. Then I had to sum for all sequences. A bit fiddly.

Part 1:

<?php

function newsecret($num1) {
  /*
  secret number s1
  multiply s1 by 64 - s2
  mix s2 into s1 - s3
  prune s3 - s4

  divide s4 by 32 - s5
  round s5 down to integer - s6
  mix s6 into into s4 - s7
  prune s7 - s8

  multiply s8 by 2048 - s9
  mix s9 into s8 - s10
  prune s10 - s11

  mix a into b: bitwise xor a and b
  prune a: a % 16777216
  */
  
  $num4 = (($num1 * 64) ^ $num1) % 16777216;
  $num8 = (floor($num4 / 32) ^ $num4) % 16777216;
  $num11 = (($num8 * 2048) ^ $num8) % 16777216;
  return $num11;
}

///////////////////////////////////////////

$input = file_get_contents('./d22input1.txt', true);
$rounds = 2000;

foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
  if(strlen($line)>0) {
    $secrets[] = (int) $line;
  }
}

$sum = 0;
foreach($secrets as $num) {
  for($i=0;$i<$rounds;$i++) {
    $num = newsecret($num);
  }
  $sum += $num;
}
print("$sum\n");
?>

Part 2:

<?php

function newsecret($num1) {
  /*
  secret number s1
  multiply s1 by 64 - s2
  mix s2 into s1 - s3
  prune s3 - s4

  divide s4 by 32 - s5
  round s5 down to integer - s6
  mix s6 into into s4 - s7
  prune s7 - s8

  multiply s8 by 2048 - s9
  mix s9 into s8 - s10
  prune s10 - s11

  mix a into b: bitwise xor a and b
  prune a: a % 16777216
  */
  
  $num4 = (($num1 * 64) ^ $num1) % 16777216;
  $num8 = (floor($num4 / 32) ^ $num4) % 16777216;
  $num11 = (($num8 * 2048) ^ $num8) % 16777216;
  return $num11;
}

///////////////////////////////////////////

$input = file_get_contents('./d22input2.txt', true);
$rounds = 2000;

foreach(preg_split("/((\r?\n)|(\r\n?))/", $input) as $line) {
  if(strlen($line)>0) {
    $secrets[] = (int) $line;
  }
}

// for each buyer
foreach($secrets as $buyer => $numx) {
  // the last 4 changes in price, init
  $numa = 0;
  $numb = 0;
  $numc = 0;
  $numd = 0;
  $numm = 0;
  // for each new secret price
  for($i=0;$i<$rounds;$i++) {
    $numy = newsecret($numx);
    $numn = $numy % 10;
    $numa = $numb;
    $numb = $numc;
    $numc = $numd;
    $numd = $numn - $numm;
    // only if we have 4 changes / 5 prices / i >= 4
    if($i>=4) {
      if(!isset($changes[$numa][$numb][$numc][$numd][$buyer])) {
        $changes[$numa][$numb][$numc][$numd][$buyer] = $numn;
      }
    }
    $numx = $numy;
    $numm = $numn;
  }
}

$bestsum = 0;
// for each sequence, calculate sum
// remember best sum
for($a=-9;$a<=9;$a++) {
  for($b=-9;$b<=9;$b++) {
    for($c=-9;$c<=9;$c++) {
      for($d=-9;$d<=9;$d++) {
        if(isset($changes[$a][$b][$c][$d])) {
          $tmpsum = array_sum($changes[$a][$b][$c][$d]);
          if($tmpsum > $bestsum) {
            $bestsum = $tmpsum;
            $bestseq = "($a,$b,$c,$d)";
          }
        }
      }
    }
  }
}

print("$bestsum $bestseq\n");

?>

A new December and a new bunch of puzzles from mscroggs.co.uk.

Without comment, the solution.

And the 3 digit number is 651.

This week the question is: Can You Break the Bell Curve?

Bean machines can famously produce bell-shaped curves. But today, we’re going to change all that!

Suppose you have a board like the one shown below. The board’s topmost row has three pins (and two slots for a ball to pass through), while the bottommost row has two pins (and three slots for a ball to pass through). The remaining rows alternate between having three pins and two pins.

But instead of the 12 rows of pins in the illustrative diagram, suppose the board has many, many rows. And at the very bottom of the board, just below the two bottommost pins, are three buckets, labeled A, B, and C from left to right. [Picture rotated counter clockwise.]

Whenever a ball encounters one of the leftmost pins, it travels down the right side of it to the next row. And whenever a ball encounters one of the rightmost pins, it travels down the left side of it to the next row.

But this isn’t your garden variety bean machine. Whenever a ball encounters any of the other pins, it has a 75 percent chance of traveling down the right side of that pin, and a 25 percent chance of traveling down the left side of that pin.

A single ball is about to be dropped into the left slot at the top of the board. What is the probability that the ball ultimately lands in bucket A, the leftmost slot at the bottom?

And for extra credit:

Suppose you have the board below, which starts with a row with six pins (and five slots), followed by a row with five pins (and six slots), and then back to six pins in an alternating pattern. Balls are only allowed to enter through the middle three slots on top. This time around, the pins that aren’t on the far left or far right behave normally, meaning each ball is equally likely to go around it via the left side or the right side.

Your goal is to create a trapezoidal distribution along one of the rows with six slots, which have been highlighted with dotted lines in the diagram above. More precisely, the frequency of balls passing through the six slots from left to right should be x−y, x, x+y, x+y, x, x−y, for some values of x and y with x ≥ y.

Suppose the ratio by which you drop balls into the top three middle slots, from left to right, is a : b : c, with a + b + c = 1. Find all ordered triples (a, b, c) that result in a trapezoidal distribution in at least one row with six slots.

Highlight to reveal (possibly incorrect) solution:

Figure 1 and 2. Program.

Assumptions:

• After many rows, the state of the bean machine will reach an equilibrium. The values for the row just above the A, B and C bins will be the same as for the 2 pin row just above that.
• This equilibrium is independent of the beginning state.

First let’s name some things. (Figure 1.)

Before reaching the last row, a ball travels through the state A’, B’ or C’. Then it goes through one of the states of the next row, let’s call them X and Y. And finally it reaches A, B or C. p(S) is the probability, that the ball reached this state, S.

p(A) = p(X) * 1/4

p(B) = p(X) * 3/4 + p(Y) * 1/4

p(C) = p(Y) * 3/4

p(X) = p(A’) + p(B’) * 1/4

p(Y) = p(B’) * 3/4 + p(C’)

Using the assumptions:

p(A) = p(A’) etc.

Further: p(A) + p(B) + p(C) = 1. WolframAlpha is happy to solve this system of equations for me. (Figure 2.)

The answer we’re looking for is p(A) = 0.025 = 1/40. A small program confirms this.

And for extra credit:

Assumptions:

• The 5 pin states converge rather quickly into (0.1, 0.2, 0.2, 0.2, 0.2, 0.1). If we want something radically different (and we do), it has to be found within the first maybe 10 pairs of rows. So let’s just look at these early, non-equilibrium states.
• We’re looking for a symmetric state (x−y, x, x+y, x+y, x, x−y). Therefore the beginning state must also be symmetric. Not (a, b, c), but (a, b, a). Therefore b = 1 – 2a, 0 <= a <= 0.5, 0 <= b, <= 1. We’re just looking for a.
• Adding up the sixth sought after probabilities, we get 6x. 6x = 1, so x = 1/6.
• A symmetric state, where the 2nd and 5th probabilities were 1/6, would represent a solution.

Let’s look at some probabilities. Each filled out cell is a position between 2 pins in a row. I only show the left part of the table, as the right part is simply a mirror of the left part. Our potential x = 1/6 will show up in the 3rd column.

	0		a		b
0		a/2		a/2+b/2
	a/4		a/2+b/4		a/2+b/2
a/8		3a/8+b/8		a/2+3b/8
	5a/16+b/16		7a/16+b/4		a/2+3b/8
5a/32+b/32		3a/8+5b/32		15a/32+3b/8
	11a/32+7b/64		27a/64+17b/64		15a/32+3b/8
11a/64+7b/128		49a/128+3b/16		57a/128+41b/128
	93a/256+19b/128		53a/128+65b/256		57a/128+41b/128
93a/512+19b/256		199a/512+103b/512		55a/128+147b/512

It is possible to have a/2 = 1/6? Yes it is, a = 1/3.

Is it possible to have 3a/8+b/8 = 1/6?

• 3a/8 + b/8 = 1/6
• 3a + b = 8/6 = 4/3
• 9a + 3b = 4
• 9a + 3(1-2a) = 4
• 9a + 3 – 6a = 4
• 3a = 1
• a = 1/3

The same solution, a = 1/3.

Is it possible to have 3a/8+5b/32 = 1/6?

• 3a/8 + 5b/32 = 1/6
• 12a + 5b = 32/6
• 72a + 30b = 32
• 72a + 30(1-2a) = 32
• 72a + 30 – 60a = 32
• 12a = 2
• a = 1/6

A new solution, a = 1/6.

Is it possible to have 49a/128+3b/16 = 1/6?

• 49a/128 + 3b/16 = 1/6
• 49a + 24b = 128/6 = 64/3
• 147a + 72b = 64
• 147a + 72(1-2a) = 64
• 147a + 72 – 144a = 64
• 3a = -8
• a = -8/3

This won’t do, a has to be positive.

Is it possible to have 199a/512+103b/512 = 1/6?

• 199a/512 + 103b/512 = 1/6
• 199a + 103b = 512/6 = 256/3
• 597a + 309b = 256
• 597a + 309(1-2a) = 256
• 597a + 309 – 618a = 256
• 53 = 21a
• a = 53/21

As we go along, we will keep getting weird solutions. Therefore the whole set of solutions is:

(1/3, 1/3, 1/3), (1/6, 2/3, 1/6).

Phew!