Anmeldelse af “Billy Baileys rebranding”, af Cory Doctorow. Novelle. 2024. Så fremmed et sted.

Skitse: Billy har været noget af en rod siden børnehaven, men hævn over Mitchell kræver en anden profil. Lad forhandlingerne med agenter og sponsorer begynde.

Er det science fiction? Ja, det er det vel egentlig. En fremtid med mere aggressive reklamer.

Temaer: Billy er helt klart intelligent, og selvom der er voksne omkring ham, så træffer han selv beslutningerne.

Er det godt? Jeps. Også lidt sjovt. 👽👽👽

Anmeldelse af “Verdens største fjols”, af Cory Doctorow. Novelle. 2024. Så fremmed et sted.

Skitse: Verdens klogeste mand har løst en masse opgaver, mens en computer har kigget med. Således kan man lave en chip, der kan gøre en anden mand lige så klog.

Er det science fiction? Ja.

Temaer: Hvad er klogskab egentlig? Kan den kloge kontrolleres af den mindre kloge?

Er det godt? Jeps. Tilfredsstillende afslutning. 👽👽👽

Anmeldelse af “Så fremmed et sted”, af Cory Doctorow. Novelle. 2024. Så fremmed et sted.

Skitse: Som 10-årig flytter vores hovedperson, James, til 1975 fra Utah. Utah i 1898 altså.

Er det science fiction? Ja.

Temaer: 1975 er ikke helt, som det skal være i vores øjne. Futuristiske materialer, transportformer, undervisning osv. Kontakt mellem årstallene bliver overvåget og kontrolleret, men åbenlyst er der stadig ting, der slipper igennem. I øvrigt er James’ far ambassadør.

James har et liv i 1898 og frem, der dog rammer 70’erne af og til. Der er lidt drama. At far en dag ikke kommer hjem fra arbejde. At mor efter noget tid finder en ny mand. At James’ lærer har en spændende baggrund og en interessant tilgang til James’ skolegang.

Der er lidt fnidder her med mangel på kolon før anførselstegn, men hvis jeg husker ret, så har den originale tekst noget lignende. Til gengæld er oversættelsen i sig selv rigtig god, ligesom i resten af bogen.

Er det godt? Jeps. 👽👽👽

Anmeldelse af “Møghund”, af Cory Doctorow. Novelle. 2024, dog også tidligere 2015. Så fremmed et sted.

Skitse: Jerry tjener bl.a. penge på at købe genstande billigt på loppemarkeder og sælge dem på auktion. Han er rigtig gode venner med Møghund, et rumvæsen, der primært samler. Indtil de har et sammenstød over en samling cowboyting for børn.

Er det science fiction? Jeps.

Temaer: Der findes jo alle slags personer, så hvorfor dog ikke også en, der støvsuger loppemarkeder for guf?

Og hvorfor skulle sådan en ikke kunne være et rumvæsen? Der normalt handler med væsentlige dyrere produkter, men det andet kan jo være en hobby. Der er et interessant fænomen her, hvor et menneske kommer i øjenhøjde med det fremmede.

Er det godt? Jeps. De ganske få tråde samles tilfredsstillende. 👽👽👽

Note: Jeg har et blødt punkt for Doctorow, så jeg giver selvfølgelig også gode karakterer til hans historier.

This week the #puzzle is: Can You See Between the Trees? #geometry

You are at the point (0, 0) on the coordinate plane. There is a tree at each point with nonnegative integer coordinates, such as (5, 6), (0, 7), and (9, 1). The trees are very thin, so that they only obstruct trees that are directly behind them. For example, the tree at (2, 2) is not visible, as it is obscured by the tree at (1, 1).

Now, you can’t see infinitely far in this forest. Suppose, for example, that the farthest you can see is 4 units. The diagram below shows the trees you would see and the angles between them:

In truth, you can see much farther than 4 units into the forest. You’re not sure exactly how far you can see, but it’s pretty dang far. To be extra clear about this, the diagram above is just an illustration, and you can in fact see much farther than 4 units.

As you look around, you can make out very narrow angular gaps between the trees. The largest gaps are near the positive x-axis and the positive y-axis (similar to the illustrated case above). After those, the next largest pair of gaps are on either side of the tree at (1, 1), 45 degrees up from the x-axis.

Consider the view between 0 and 45 degrees up from the x-axis. The next largest pair of adjacent gaps in this range are on either side of what angle up from the x-axis? (To be clear, you are not considering the gap just above 0 degrees or the gap just below 45 degrees.)

And for extra credit:

The fifth largest pair of adjacent gaps in this range are on either side of what angle up from the x-axis? (Again, you are not considering the gap just above 0 degrees or the gap just below 45 degrees.)

Highlight to reveal (possibly incorrect) solution:

Program. Spreadsheet.

To get a sense of the problem, I made a spreadsheet and played around with it a little. Then I wrote a program, that could easily handle much bigger distances. The answer seems to be the angle is 26.56505. This is the angle corresponding to (2,1).

(Observation: the big gaps occur around angles with a lot of potential hits. In this case (2,1), (4,2), (6,3) etc. There’s a lot of hits, because the first pair of coordinates have low values (2 and 1).)

And for extra credit:

Same program. The 5th pair of gaps, sorted on size, occurs at the angle 36.86990. This is the angle corresponding to (4,3).

I’ve recently read Doomsday Book, Connie Willis. These notes are about an aspect of the book, I didn’t really like. Spoilers.

Of course it’s drama and conflict. Of course our hero wants something and can’t get it right away. It’s the obstacles I, ahem, stumble over.

You can’t get what you want:

• Because you fell ill. Really ill.
• Because somebody else fell ill. Really ill.
• Because a lot of people fell ill and quarantine rules apply.
• Because somebody else has to authorise it, and they are on vacation for 2 weeks and impossible to find.
• Because somebody else has to authorise it, and they are arrogant and won’t listen to reason. (*)
• Because your question (or the answer) isn’t understood correctly.
• Because you talking to the other relevant person Just Isn’t Done, and you can’t figure out a way to do it in secret.
• Because your sense of duty says you should do something else.
• Because a 5 year old is being 5 and spoiled.
• Because a 12 year old is trying to stay away from that creepy guy.
• Because young people just don’t listen. (*)
• Because this one person is suspicious and schizophrenic and generally angry and negative. (*)
• Because this one person is overly protective of her son. (*)
• Because this one person thinks cheering up = listening to horrible Bible stories. (*)

The (*) means this rubs me the wrong way. Stupid, irrational people not listening. It’s supposed to be funny? Instead it bores me. And it happens a lot.

This week the #puzzle is: Can You Throw the Hammer? #probabilities #game

You and your opponent are competing in a golf match. On any given hole you play, each of you has a 50 percent chance of winning the hole (and a zero percent chance of tying). That said, scorekeeping in this match is a little different from the norm.

Each hole is worth 1 point. Before starting each hole, either you or your opponent can “throw the hammer.” When the hammer has been thrown, whoever did not throw the hammer must either accept the hammer or reject it. If they accept the hammer, the hole is worth 2 points. If they reject the hammer, they concede the hole and its 1 point to their opponent. Both players can throw the hammer on as many holes as they wish. (Should both players decide to throw the hammer at the exact same time—something that can’t be planned in advance—the hole is worth 2 points.)

The first player to reach 3 points wins the match. Suppose all players always make rational decisions to maximize their own chances of winning.

Good news! You have won the first hole, and now lead 1-0. What is your probability of winning the match?

And for extra credit:

Instead of playing to 3 points, now the first player to 5 points wins the match.

Good news (again)! You have won the first hole, and now lead 1-0. What is your probability of winning the match?

Highlight to reveal (possibly incorrect) solution:

Program.

My own way of saying the above:

• The players are Alice (playing for me) and Bob.
• For any given hole, for any player X, p(X wins) = 50%.
• Each win is worth 1 point, unless a hammer is thrown and accepted, in which case it’s worth 2 points.
• A player can decide to throw a hammer.
• A player can decide to accept or reject a thrown hammer. Rejecting a hammer is the same as losing, worth 1 point.
• If both players throw hammers, it counts as an accepted hammer.
• One player throwing a hammer and the other accepting is equivalent to both players throwing hammers at the same time.
• The winner of the whole match is the first to reach 3 points.
• Players choose the optimal strategy.
• Alice won the first hole, and is in front 1-0.
• What is probability that Alice will win?
• The notation P_x,y is adopted to mean: the probability Alice will win when the match is at x-y. So we’re looking for P_1,0.
• A strategy consists of these choices: Given x-y, should Alice throw the hammer, or, if the hammer is thrown by Bob, accept or reject?
• In a table for P_x,y, choosing the optimal strategy for Alice, I can also see P_y,x and the optimal strategy for Bob.

Trivially, P_3+,y = 1 and P_x,3+ = 0.

With this in mind, let’s look at a table for P_2,2. Alice has the choices in the left column, Bob has the choices in the top row.

(My tables don’t quite reflect, that accept/reject occurs before the hole is played. I try to capture this nuance in the text instead. It’s important, because a match may be decided right there.)

Bob
P2,2
Alice	accept	reject	hammer
accept	50% * P3,2 + 50% * P2,3 = 50% * 1 + 50% * 0 = 50%	50% * P3,2 + 50% * P2,3 = 50% * 1 + 50% * 0 = 50%	50% * P4,2 + 50% * P2,4 = 50% * 1 + 50% * 0 = 50%
reject	50% * P3,2 + 50% * P2,3 = 50% * 1 + 50% * 0 = 50%	50% * P3,2 + 50% * P2,3 = 50% * 1 + 50% * 0 = 50%	P2,3 = 0
hammer	50% * P4,2 + 50% * P2,4 = 50% * 1 + 50% * 0 = 50%	P3,2 = 1	50% * P4,2 + 50% * P2,4 = 50% * 1 + 50% * 0 = 50%

First, let’s notice, that if player X throws a hammer, player Y should never reject, as that leads to instant defeat. Therefore the middle column and middle row drop out.

Alice has to choose the best row out of (50, 50) and (50, 50). As long as she accepts a thrown hammer, it doesn’t matter what she chooses otherwise.

P_2,2 = 50%.

Bob
P2,1
Alice	accept	reject	hammer
accept	50% * P3,1 + 50% * P2,2 = 50% * 1 + 50% * 50% = 75%	50% * P3,1 + 50% * P2,2 = 50% * 1 + 50% * 50% = 75%	50% * P4,1 + 50% * P2,3 = 50% * 1 + 50% * 0 = 50%
reject	50% * P3,1 + 50% * P2,2 = 50% * 1 + 50% * 50% = 75%	50% * P3,1 + 50% * P2,2 = 50% * 1 + 50% * 50% = 75%	P2,2 = 50%
hammer	50% * P4,1 + 50% * P2,3 = 50% * 1 + 50% * 0 = 50%	P3,1 = 1	50% * P4,1 + 50% * P2,3 = 50% * 1 + 50% * 0 = 50%

Bob is trying to choose the optimal (i.e. lowest) column from (75, 75, 50), (75, 75, 1) and (50, 50, 50). He will choose the third one and therefore throw a hammer.

P_1,2 = 50%.

Knowing Bob will throw a hammer, it doesn’t really matter what Alice chooses. All her choices give 50%.

P_2,1 = 50%.

Bob
P2,0
Alice	accept	reject	hammer
accept	50% * P3,0 + 50% * P2,1 = 50% * 1 + 50% * 50 % = 75%	50% * P3,0 + 50% * P2,1 = 50% * 1 + 50% * 50 % = 75%	50% * P4,0 + 50% * P2,2 = 50% * 1 + 50% * 50% = 75%
reject	50% * P3,0 + 50% * P2,1 = 50% * 1 + 50% * 50 % = 75%	50% * P3,0 + 50% * P2,1 = 50% * 1 + 50% * 50 % = 75%	P2,1 = 50%
hammer	50% * P4,0 + 50% * P2,2 = 50% * 1 + 50% * 50% = 75%	P3,0 = 1	50% * P4,0 + 50% * P2,2 = 50% * 1 + 50% * 50% = 75%

Alice wants the best row of (75, 75, 75), (75, 75, 50) and (75, 1, 75). This is the third row, so she throws a hammer.

Bob wants the best column of (75, 75, 75), (75, 75, 1) and (75, 50, 75). This is the third column, so he throws a hammer.

We end up in the situation where both throw a hammer.

P_2,0 = 75%.

P_0,2 = 25%.

Bob
P1,1
Alice	accept	reject	hammer
accept	50% * P2,1 + 50% * P1,2 = 50% * 50% + 50% * 50% = 50%	50% * P2,1 + 50% * P1,2 = 50% * 50% + 50% * 50% = 50%	50% * P3,1 + 50% * P1,3 = 50% * 1 + 50% * 0 = 50%
reject	50% * P2,1 + 50% * P1,2 = 50% * 50% + 50% * 50% = 50%	50% * P2,1 + 50% * P1,2 = 50% * 50% + 50% * 50% = 50%	P1,2 = 50%
hammer	50% * P3,1 + 50% * P1,3 = 50% * 1 + 50% * 0 = 50%	P2,1 = 50%	50% * P3,1 + 50% * P1,3 = 50% * 1 + 50% * 0 = 50%

Everything is 50%. Either player can do anything.

P_1,1 = 50%.

Bob
P1,0
Alice	accept	reject	hammer
accept	50% * P2,0 + 50% * P1,1 = 50% * 75% + 50% * 50% = 62.5%	50% * P2,0 + 50% * P1,1 = 50% * 75% + 50% * 50% = 62.5%	50% * P3,0 + 50% * P1,2 = 50% * 1 + 50% * 50% = 75%
reject	50% * P2,0 + 50% * P1,1 = 50% * 75% + 50% * 50% = 62.5%	50% * P2,0 + 50% * P1,1 = 50% * 75% + 50% * 50% = 62.5%	P1,1 = 50%
hammer	50% * P3,0 + 50% * P1,2 = 50% * 1 + 50% * 50% = 75%	P2,0 = 75%	50% * P3,0 + 50% * P1,2 = 50% * 1 + 50% * 50% = 75%

The best row for Alice is the third, and she throws a hammer.

P_1,0 = 75%.

The best columns for Bob are those where he doesn’t throw a hammer. Given that Alice does throw one, he ends up in the bottom row.

P_0,1 = 25%.

Oh! We’ve actually found the value, we were looking for. P_1,0 = 75%.

Just to make sure, I also wrote a program to confirm this (and the next) result.

And for extra credit:

Everything is the same, we’re just going for a win of 5 instead of 3.

Trivially, P_5+,y = 1 and P_x,5+ = 0.

If we read P_x,y in the fiddler as “Alice is 3-x away from having 3 points and Bob is 3-y away”, we can translate all of this into P_x+2,y+2 for this extra credit puzzle.

P4,4 = 50%	P2,4 = 25%
P3,4 = 50%	P3,3 = 50%
P4,3 = 50%	P3,2 = 75%
P4,2 = 75%	P2,3 = 25%

Having established that, let’s move forward.

Bob
P4,1
Alice	accept	reject	hammer
accept	50% * P5,1 + 50% * P4,2 = 50% * 1 + 50% * 75% = 62.5%	50% * P5,1 + 50% * P4,2 = 50% * 1 + 50% * 75% = 62.5%	50% * P6,1 + 50% * P4,3 = 50% * 1 + 50% * 50% = 75%
reject	50% * P5,1 + 50% * P4,2 = 50% * 1 + 50% * 75% = 62.5%	50% * P5,1 + 50% * P4,2 = 50% * 1 + 50% * 75% = 62.5%	P4,2 = 75%
hammer	50% * P6,1 + 50% * P4,3 = 50% * 1 + 50% * 50% = 75%	P5,1 = 1	50% * P6,1 + 50% * P4,3 = 50% * 1 + 50% * 50% = 75%

The best row for Alice is the 3rd, throwing a hammer.

Given this, and rejecting a hammer would be a losing strategy, the best column for Bob is the 1st, accepting a hammer.

P_4,1 = 75%. P_1,4 = 25%.

Bob
P4,0
Alice	accept	reject	hammer
accept	50% * P5,0 + 50% * P4,1 = 50% * 1 + 50% * 75% = 87.5%	50% * P5,0 + 50% * P4,1 = 50% * 1 + 50% * 75% = 87.5%	50% * P6,0 + 50% * P4,2 = 50% * 1 + 50% * 75% = 87.5%
reject	50% * P5,0 + 50% * P4,1 = 50% * 1 + 50% * 75% = 87.5%	50% * P5,0 + 50% * P4,1 = 50% * 1 + 50% * 75% = 87.5%	P4,1 = 75%
hammer	50% * P6,0 + 50% * P4,2 = 50% * 1 + 50% * 75% = 87.5%	P5,0 = 1	50% * P6,0 + 50% * P4,2 = 50% * 1 + 50% * 75% = 87.5%

The best row for Alice is 3rd, she throws a hammer.

The best column for Bob is the 3rd, he throws a hammer.

P_4,0 = 87.5%. P_0,4 = 12.5%.

Bob
P3,1
Alice	accept	reject	hammer
accept	50% * P4,1 + 50% * P3,2 = 50% * 75% + 50% * 75% = 75%	50% * P4,1 + 50% * P3,2 = 50% * 75% + 50% * 75% = 75%	50% * P5,1 + 50% * P3,3 = 50% * 1 + 50% * 50% = 75%
reject	50% * P4,1 + 50% * P3,2 = 50% * 75% + 50% * 75% = 75%	50% * P4,1 + 50% * P3,2 = 50% * 75% + 50% * 75% = 75%	P3,2 = 75%
hammer	50% * P5,1 + 50% * P3,3 = 50% * 1 + 50% * 50% = 75%	P4,1 = 75%	50% * P5,1 + 50% * P3,3 = 50% * 1 + 50% * 50% = 75%

Everything is 75%. Either player can do anything.

P_3,1 = 75%. P_1,3 = 25%.

Bob
P2,2
Alice	accept	reject	hammer
accept	50% * P3,2 + 50% * P2,3 = 50% * 75% + 50% * 25% = 50%	50% * P3,2 + 50% * P2,3 = 50% * 75% + 50% * 25% = 50%	50% * P4,2 + 50% * P2,4 = 50% * 75% + 50% * 25% = 50%
reject	50% * P3,2 + 50% * P2,3 = 50% * 75% + 50% * 25% = 50%	50% * P3,2 + 50% * P2,3 = 50% * 75% + 50% * 25% = 50%	P2,3 = 25%
hammer	50% * P4,2 + 50% * P2,4 = 50% * 75% + 50% * 25% = 50%	P3,2 = 75%	50% * P4,2 + 50% * P2,4 = 50% * 75% + 50% * 25% = 50%

The best row for Alice is the 3rd. She throws a hammer.

The best column for Bob is the 3rd. He throws a hammer.

P_2,2 = 50%.

Bob
P3,0
Alice	accept	reject	hammer
accept	50% * P4,0 + 50% * P3,1 = 50% * 87.5% + 50% * 75% = 81.25%	50% * P4,0 + 50% * P3,1 = 50% * 87.5% + 50% * 75% = 81.25%	50% * P5,0 + 50% * P3,2 = 50% * 1 + 50% * 75% = 87.5%
reject	50% * P4,0 + 50% * P3,1 = 50% * 87.5% + 50% * 75% = 81.25%	50% * P4,0 + 50% * P3,1 = 50% * 87.5% + 50% * 75% = 81.25%	P3,1 = 75%
hammer	50% * P5,0 + 50% * P3,2 = 50% * 1 + 50% * 75% = 87.5%	P4,0 = 87.5%	50% * P5,0 + 50% * P3,2 = 50% * 1 + 50% * 75% = 87.5%

For Alice the 3rd row is best. She throws a hammer.

Knowing this, it doesn’t matter what Bob does.

P_3,0 = 87.5%. P_0,3 = 12.5%.

Bob
P2,1
Alice	accept	reject	hammer
accept	50% * P3,1 + 50% * P2,2 = 50% * 75% + 50% * 50% = 62.5%	50% * P3,1 + 50% * P2,2 = 50% * 75% + 50% * 50% = 62.5%	50% * P4,1 + 50% * P2,3 = 50% * 75% + 50% * 25% = 50%
reject	50% * P3,1 + 50% * P2,2 = 50% * 75% + 50% * 50% = 62.5%	50% * P3,1 + 50% * P2,2 = 50% * 75% + 50% * 50% = 62.5%	P2,2 = 50%
hammer	50% * P4,1 + 50% * P2,3 = 50% * 75% + 50% * 25% = 50%	P3,1 = 75%	50% * P4,1 + 50% * P2,3 = 50% * 75% + 50% * 25% = 50%

For Bob the best column is the 3rd. He throws a hammer.

Given this, it doesn’t matter what Alice chooses.

P_2,1 = 50%. P_1,2 = 50%.

Bob
P2,0
Alice	accept	reject	hammer
accept	50% * P3,0 + 50% * P2,1 = 50% * 87.5% + 50% * 50% = 68.75%	50% * P3,0 + 50% * P2,1 = 50% * 87.5% + 50% * 50% = 68.75%	50% * P4,0 + 50% * P2,2 = 50% * 87.5 + 50% * 50% = 68.75%
reject	50% * P3,0 + 50% * P2,1 = 50% * 87.5% + 50% * 50% = 68.75%	50% * P3,0 + 50% * P2,1 = 50% * 87.5% + 50% * 50% = 68.75%	P2,1 = 50%
hammer	50% * P4,0 + 50% * P2,2 = 50% * 87.5 + 50% * 50% = 68.75%	P3,0 = 87.5%	50% * P4,0 + 50% * P2,2 = 50% * 87.5 + 50% * 50% = 68.75%

For Alice the best row is the 3rd. She throws a hammer.

Knowing this, Bob just avoids rejecting it.

P_2,0 = 68.75%. P_0,2 = 31.25%.

Almost there!

For symmetry reasons, P_1,1 = 50%.

Bob
P1,0
Alice	accept	reject	hammer
accept	50% * P2,0 + 50% * P1,1 = 50% * 68.75% + 50% * 50% = 59.375%	50% * P2,0 + 50% * P1,1 = 50% * 68.75% + 50% * 50% = 59.375%	50% * P3,0 + 50% * P1,2 = 50% * 87.5 + 50% * 50% = 68.75%
reject	50% * P2,0 + 50% * P1,1 = 50% * 68.75% + 50% * 50% = 59.375%	50% * P2,0 + 50% * P1,1 = 50% * 68.75% + 50% * 50% = 59.375%	P1,1 = 50%
hammer	50% * P3,0 + 50% * P1,2 = 50% * 87.5 + 50% * 50% = 68.75%	P2,0 = 68.75%	50% * P3,0 + 50% * P1,2 = 50% * 87.5 + 50% * 50% = 68.75%

Alice throws a hammer.

Bob doesn’t reject.

P_1,0 = 68.75%.

This week the question is: Can You Grow a Hibiscus Hedge? #permutation #sequence

Dean has three colors of the hibiscus: red, orange, and yellow. He wants to plant them in a straight hedge of shrubs (each of which is one color) so that the order appears somewhat random, but not truly random. More specifically, he wants the following to be true:

– No two adjacent shrubs have the same color. – No ordering of three consecutive shrubs appears more than once in the hedge. (But a prior ordering can appear in reverse. For example, ROYOR is an acceptable hedge, but ROYROY is not.)

What is the greatest number of shrubs Dean’s hedge can contain?

And for extra credit:

In addition to red, orange, and yellow hibiscus flowers, Dean now includes a fourth color: pink. Again, he wants to plant a straight hedge of shrubs that appears somewhat random. Here are the rules for ordering the shrubs this time:

– No two adjacent shrubs have the same color. – No ordering of four consecutive shrubs appears more than once in the hedge. (Again, a prior ordering can appear in reverse.) – Among any group of four consecutive shrubs, at least three distinct colors are represented.

What is the greatest number of shrubs Dean’s hedge can contain?

Intermission.

I am sort of obsessed with the candy puzzle from last week. Handled correctly, it’s possible to see, that the important graph has a structure, and that this structure can be used to find the required path. (This picture has a few connections missing, but hopefully it still demonstrates the principle.)

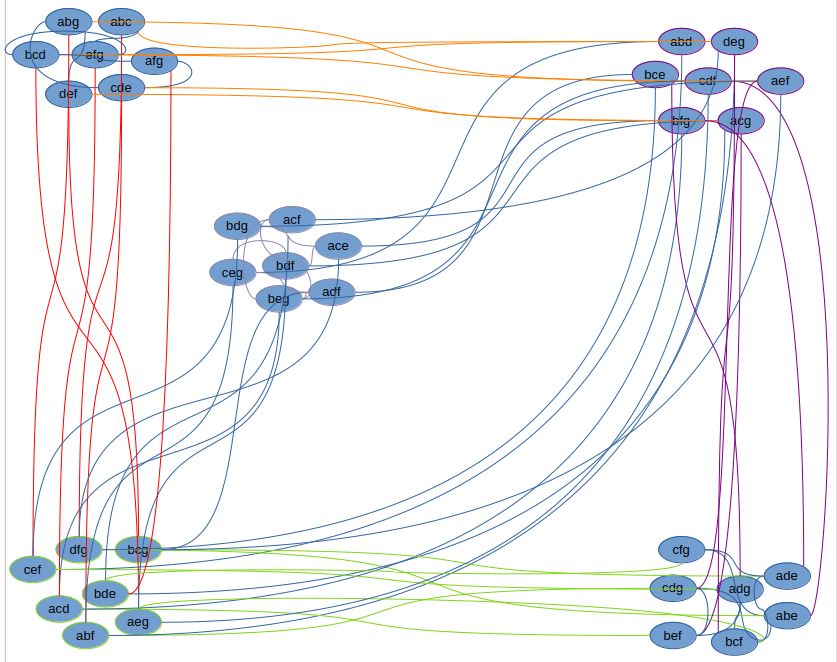
Oh! And I’ve just discovered that years ago a similar puzzle was featured on the riddler. Scroll down to the classic solution.

Last week I had to guess at the solution to the extra credit question. As it happens, I had the right idea: 21 students. But that wasn’t what the question actually asked for. Sigh. Read the question carefully, next time, me! Anyway. I got 21 points out of 26 possible in Q1. Actually not bad.

Highlight to reveal (possibly incorrect) solution:

Related problem. Program.

What are we actually looking for here?

We are interested in the permutations of the 3 colors with 3 elements. However, a permutation cannot have 2 neighbors with the same color. And in the final sequence, a permutation can appear at most once.

My program (brute forcing all possible sequences) tells me, 1) there are 12 of these permutations, 2) it is possible to build a sequence with all of them, and this sequence therefore has length 14.

One possible sequence: ROROYRYOYORYRO.

And for extra credit:

Now there are 4 colors and the permutations have 4 elements. As an extra requirement, each permutation has at least 3 colors. (Having a similar requirement doesn’t change anything in the fiddler case.)

My program tells me, 1) there are 96 of these permutations, 2) it is possible to build a sequence with all of them, and this sequence therefore has length 99.

One possible sequence (split up in smaller chunks for readability):

RORYRORPRO
YROYOROYPR
OPRYRPRYOR
YOYRYOPRPO
ROPORYPRYP
ORPOYRPOPY
ROPYORPYRY
PYRPYOYPOY
OPOYPYOPYP
RPYPOPROR

I’ve just finished reading #RedMars . A lot can be said about this book. These notes will be about just 3 topics, because I spent extra energy on them. 2 of these topics are actually topics discussed by the characters, so many times, in so many forms. It was a bit confusing for me, until I realized all those discussions were actually related. The 3rd topic is an attempt to create a #timeline .

Society, decision making:

• Like Earth? Capitalism? Democracy? Communism?
• Something new?
• Leaderless?
• Controlled from Earth?
• Independent?

Terraforming:

• Yes/no.
• Fast/slow.
• How exactly?

Timeline:

Time	Plot
Summer of 2020	Boone becomes the first man on Mars.
2022?	The selection process for the 1st 100 begins, lasting years before the move to Antarctica.
2024?	Construction of the ship to take the 1st 100 to Mars begins, lasting less than 2 years.
2025?	The 1st 100 and others live in Antarctica for 1 year.
July 20th, 2026	The 9 month voyage from Earth to Mars begins.
	The colonists use a new calendar. Ls goes from 0 to 360, and then starts over. A martian year is 668.6 local days long. This is split into Ls 0-90 (northern spring), 90-180 (northern summer), 180-270 (northern fall) and 270-360 (northern winter).
April, 2027	The 1st 100 land on Ls = 7.
2029	The dirigible Arrowhead is sent from Earth, like a lot of other provisions keep coming.
2031?	Children, all about 3 years old. The hidden colony is founded.
2033?	Chalmers becomes US Secretary.
2037?	Russell is named scientific head of the terraforming effort. Boone starts working for him.
2043?	Arabs arrives on Mars 10 years before Nicosia dedication ceremony.
2044?	UNOMA headquarters is established in Burroughs.
2047 / m-year 10	Boone tries to figure out who’s responsible for actions of sabotage. Chalmers has been US Secretary for 3 administrations. There are 10,000 colonists.
2048 / m-year 11	Rejuvenation technique begins use. The great storm begins.
2050?	The great storm ends after 3 years, 2 m-years. Construction on the space elevator begins.
2053?	Nicosia dedication ceremony. The first town of any size to be built free-standing on the martian surface. 5000 people. 25 years of friendship (beginning 2026).
February 6th, 2057 / Ls = 144, m-16	The walk on the bridge, an important bit of the negotiation of the new Mars treaty.
June 2057	The treaty is signed.
July 2057	Chalmers begins a 2 year “vacation”.
2059	Chalmers returns to work, frustrated that the treaty isn’t followed. 1,000,000 people on Mars. Less than 1% of the surface habitable.
	Revolution.

There’s an intriguing timeline elsewhere.

This week the question is: Can You Solve a High Schooler’s Favorite Puzzle?

A teacher is handing out candy to his students, of which there are at least four. He abides by the following rules:

• He hands out candy to groups of three students (i.e., “trios”) at a time. Each member of the trio gets one piece of candy.
• Each unique trio can ask for candy, but that same trio can’t come back for seconds. If students in the trio want more candy, they must return as part of a different trio.
• When a trio gets candy, the next trio can’t contain any students from that previous trio.

It turns out that every possible trio can get a helping of candy. What is the smallest class size for which this is possible?

And for extra credit:

Instead of trios of students, suppose now that groups of 10 students come up to get candy. This time, there are at least 11 students in the class. As before:

• Each member of the group of 10 gets one piece of candy per visit.
• Each unique group of 10 can ask for candy, but the exact same group of 10 can’t come back for seconds. If students in the group want more candy, they must return as part of a different group.
• When a group of 10 gets candy, the next group of 10 can’t contain any students from the previous group of 10.

Suppose the class size is the minimum that allows every possible group of 10 to get a helping of candy. How many pieces of candy does each student receive?

Highlight to reveal (possibly incorrect) solution:

Program.

The first trio could be ABC. The next trio could be DEF. The next trio can’t contain any of D, E or F, and it can’t contain all of A, B and C, so there has to be 1 more student: G. So we need at least 7 students.

(If you want to, you can name the students Annie, Bob etc.)

I wrote a program to test this theory, and found a solution. There has to be at least 7 students, and a solution with 7 students exists. We need 7 students.

Solution: abc def abg cde abf deg acf bde acg bdf ceg abd cef bdg ace bfg acd efg bcd afg bce dfg abe cfg ade bcf adg bef cdg aef bcg adf beg cdf aeg. But this isn’t the only one, as far as I can tell.

And for extra credit:

I am not sure. I’ve been trying to find a pattern in the trio solution, some way to expand this solution to 10 students in each group. No such luck. So I’ve made a guess: 21.