#ThisWeeksFiddler, 20260213

Skriv en kommentar

This week the #puzzle is: Can You Get the Rover Home? #trigonometry #spherical #3d #animation #desmos3d

A rover is dropped down on a spherical planet with a radius of 1000 miles. The rover has been programmed with a very specific set of motions:
– First, it moves straight forward a fixed distance s, and stops.
– Without moving forward, it turns left 60 degrees. (Importantly, the rover turns 60 degrees, not 120 degrees.)
– Next, the rover moves straight forward in this new direction another distance s, and stops.
– Without moving forward, it again turns left 60 degrees.
– Finally, the rover moves straight forward in this new direction another distance s, and stops.
To be picked up, the rover must complete its journey in the same place it was dropped down. What is the minimum value of s, with s > 0, for which this works?
To help you out, here’s an illustration, courtesy of Pierre, of what such a path might look like:

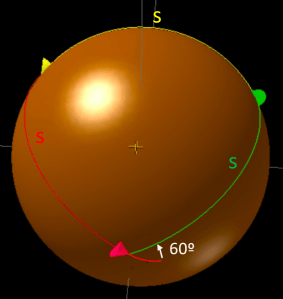And for extra credit:

There are other values of s for which the rover will end its journey where it was dropped down. How many such positive values of s (including the answer you just found in the Fiddler) are less than 100,000 miles?

Can You Get the Rover Home?

Possibly incorrect solution:

Method 1: Turns out there’s a Spherical law of cosines! Who knew! This law says:

cos(c)=cos(a)cos(b)+sin(a)sin(b)cos(C)cos(c)=cos(a)cos(b)+sin(a)sin(b)cos(C)

In our case:

a=b=c=s1000a=b=c=\frac{s}{1000}

C=120°C=120 \degree

So we’re just looking for s.

cos(s1000)=cos(s1000)cos(s1000)+sin(s1000)sin(s1000)(−12)cos(\frac{s}{1000})=cos(\frac{s}{1000})cos(\frac{s}{1000})+sin(\frac{s}{1000})sin(\frac{s}{1000})(-\frac{1}{2})

Solutions:

s1n=2(πn−tan−1(2))1000s_{1n}=2(\pi n – tan^{-1}(\sqrt{2}))1000

s2n=2πn1000s_{2n}=2 \pi n 1000

s3n=2(πn+tan−1(2))1000s_{3n}=2(\pi n + tan^{-1}(\sqrt{2}))1000

In our case the most interesting solution is this one:

s30=2(π0+tan−1(2))1000≈1911s_{30}=2(\pi 0 + tan^{-1}(\sqrt{2}))1000 \approx1911

Method 2: I looked at the sphere is Desmos . Looks good.

Result: 1911 miles.

Animations

I have made animations of the 3 situations! I am insanely proud of them!

Desmos 6 , Desmos 7 , Desmos 8 .

And for extra credit:

Method 1: The solutions are clustered around:

2πn10002 \pi n 1000

The next 3 solutions are:

4373,6238,81944373, 6238, 8194

The 3rd solution of these is a replica of the fiddler solution, it just goes all the way around the planet before taking the 1911 miles.

The 2nd solution is going all the way around the planet to the starting point. The trivial one.

The 1st solution emulates the fiddler. Imagine a fiddler solution. Start at one of the corners. Then instead of going to the next corner, go in the opposite direction, away from the triangle, going around the planet and arriving at the next corner. Etc.

There will be a set of solutions for n = 15:

92337,94247,9615892337, 94247, 96158

And a partial set for n = 16:

9862098620

And then the values grow larger than 100000.

So there’s 1 + 15 * 3 + 1 solutions.

Method 2: I also looked at these solutions in Desmos.

Result: 47 solutions.

Skriv en kommentar