This week the #puzzle is: Can You Brighten Up the Room? #geometry #trigonometry #angles #reflection #animation

While dining at a restaurant, I notice a lamp descending from the ceiling, as shown in the diagram below. The lamp consists of a point light source at the center of a spherical bulb with a radius of 1 foot. The top half of the sphere is opaque. The bottom half of the sphere is semi-transparent, allowing light out (and thus illuminating my table) but not back in. The light source itself is halfway up to the ceiling—5 feet off the ground and 5 feet from the ceiling. The ground reflects light.

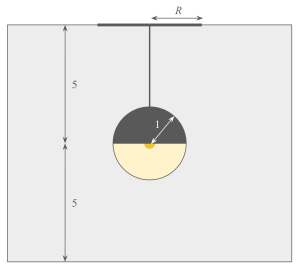Above the light, on the ceiling, I see a circular shadow. What is the radius R of this shadow?

And for extra credit:

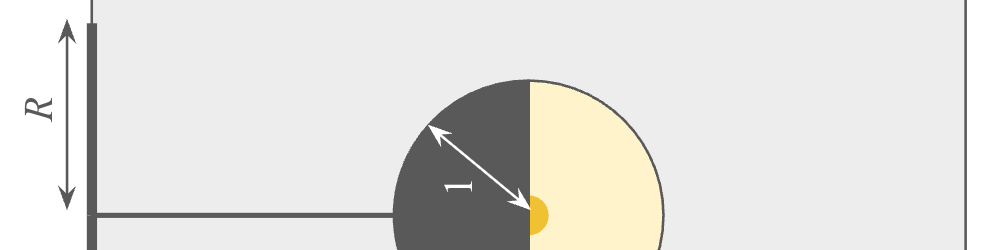
Now suppose the lamp has a radius r and is suspended a height h off the ground in a room with height 2h. Again, the radius of the shadow on the ceiling is R.

For whatever reason, the restaurant’s architect insists that she wants r, h, and R, as measured in feet, to all be whole numbers. What is the smallest value of R for which this is possible?

Can You Brighten Up the Room?

Highlight to reveal (possibly incorrect) solution:

Desmos

Thoughts:

• Playing around with Desmos a little shows, that we want to find, where light hits the floor and reflects back and just nicks the lamp.
• The light will travel 5 feet down and then 5 up. Meanwhile it will travel 1 foot horizontally.
• After nicking the lamp, it will travel a further 5 up and 0.5 horizontally.
• It will hit the light 1.5 feet away from the center. This is the radius of the shadow.
• Playing with the angle of the light, I find a solution when the angle is 4.6122 rad and the radius is 1.507556 feet.

And for extra credit:

Program Animation

Thoughts:

• Originally we had r = 1 and h = 5, resulting in R = 1.5.
• We want different values for r, h and R, so that they are all integers and R is minimized.
• I don’t think h actually matters.
• R = 1.5 * r.
• r should be an integer n, and so should 1.5 * n.
• 1.5 * n
  • = 3/2 * n
  • = 3 * n/2
• So n should be divisible by 2.
• We minimize R by minimizing r.
• The solution seems to be r = 2, R = 3. (And then h = 5 or whatever.)

Ahem.

• Originally we had r = 1 and h = 5, resulting in R = 1.507556. This happens at angle k = 4.6122216 rad.
• R = 3 * h / tan(k)
• Furthermore the distance between the line nicking the lamp and (0,0) has to be 1.
• The second part of the light beam is represented by y = tan(k) * x – 2 * h.
• x² + y² = 1 and y = tan(k) * x – 2 * h
  • <=> x² + (tan(k) * x – 2 * h)² = 1
  • <=> x² + tan²(k) * x² – 4 * h * tan(k) * x + 4h² = 1
  • <=> (tan²(k) + 1) * x² – 4 * h * tan(k) * x + 4h² – 1 = 0
  • <=> x = (4 * h * tan(k) +- √((4 * h * tan(k))² – 4 * (tan²(k) + 1) * (4h² – 1))) / (2 * (tan²(k) + 1))
  • <=> x = (4 * h * tan(k) +- √(4² * h² * tan²(k) – 4 * (tan²(k) + 1) * (4h² – 1))) / (2 * (tan²(k) + 1))
  • <=> x = (2 * h * tan(k) +- √(4 * h² * tan²(k) – (tan²(k) + 1) * (4h² – 1))) / (tan²(k) + 1)
  • <=> x = (2 * h * tan(k) +- √(4 * h² * tan²(k) – tan²(k) (4h² – 1) – 4h² – 1)) / (tan²(k) + 1)
  • <=> x = (2 * h * tan(k) +- √(tan²(k) – 4h² + 1)) / (tan²(k) + 1)
• We want this to only have 1 solution.
• tan²(k) – 4h² + 1 = 0
  • <=> tan²(k) = 4h² – 1
  • <=> tan(k) = √(4h² – 1)
  • <=> k = arctan(√(4h² – 1))
• Just to test: h = 5, k = 1.47063. k + π = 4.61222.

This actually assumes r = 1. Let’s try again.

• R = r * 3 * h / tan(k)
• The result for k becomes:
• k = arctan(√(4h² – r²))
• Therefore:
• R = r * 3 * h / tan(arctan(√(4h² – r²)))
  • = r * 3 * h / √(4h² – r²)
• So. We want h, r and R all to be integer.
• First we need 4h² – r² to be a square.
• Let r = 2m
• 4h² – r² = 4h² – (2m)²
  • 4h² – 4m²
  • 4(h² – m²)
• This is a square when h² – m² is square.
• h > m, squares have to be positive. (Also, we don’t want to lamp to hit the floor, so h > 2m.)
• h² – m² = a²
  • <=> h² = a² + m²
• h, m and a are all integer. (r is even.)
• Example: m = 5, a = 12, h = 13.
• h = 13, r = 2m = 10
• 4h² – r² = 4 * 13² – 10²
  • = 576
• R = r * 3 * h / √(4h² – r²)
  • 10 * 3 * 13 / √576
  • 390 / 24
  • 16.25
• So that wasn’t actually enough.
• a has to divide r * 3 * h
• R = r * 3 * h / √(4h² – r²)
  • = 2m * 3 * h / √(4h² – (2m)²)
  • = 2m * 3 * h / √(4 * (h² – m²))
  • = 2m * 3 * h / √(4 * a²)
  • = 2m * 3 * h / 2√(a²)
  • = 3mh / a
• I think it’s time to write a program.

My program finds several possible solutions.

r: 40	h: 52	R: 65.0000
r: 80	h: 85	R: 136.0000
r: 80	h: 104	R: 130.0000
r: 112	h: 200	R: 175.0000
r: 120	h: 156	R: 195.0000
r: 160	h: 170	R: 272.0000
r: 160	h: 208	R: 260.0000
r: 200	h: 260	R: 325.0000
r: 224	h: 400	R: 350.0000
r: 240	h: 255	R: 408.0000
r: 240	h: 312	R: 390.0000
r: 280	h: 364	R: 455.0000
r: 320	h: 340	R: 544.0000
r: 320	h: 416	R: 520.0000
r: 360	h: 468	R: 585.0000
r: 400	h: 425	R: 680.0000

Oh, and I did an animation of some of the solutions. Baby’s first animation.

From this I find, that R = 65 feet is the smallest solution.