I’ve done Everybody Codes, back in November.

The Song of Ducks and Dragons [ 2025 ]

All my code is available . And so are my times. And I really like, that we operate with local times here.

.........................................................................................#
.................#...........#.....#........#........#.....#...........#.................#
.....#..##.#..#..#.#...#..#..#.....#...#.#..#..#.#...#.....#..#..#...#.#..#..#.##..#.....#
.#####.###.#.###.#.###.#####.#.#####.###.#.###.#.###.#####.#.#####.###.#.###.#.###.#####.#
##########################################################################################

Quest 16. There’s a certain kind of wall, with a connection between a list of numbers, a given length and the resulting wall built by a known number of blocks. For the list of numbers, 1 means, place a block in every column. 9 means, place a block every 9 columns. Given a list of numbers and a length, count all the blocks (part 1). Given a known wall, find the list (part 2). Given a known wall segment and a number of blocks, find the length (part 3).

Oh, the circularity! Part 1 uses floor(). For part 2, I can reverse engineer the wall. Is there a block in column 1? Add 1 to the list of numbers and mark all the corresponding blocks. Is there an unmarked block in column 2? Add 2 to the list of numbers and mark blocks. Is there an unmarked block in column 3? Add 3 to the list… For part 3, bisection is good.

..........4..........
......473483436......
....4671465878781....
...219317375373724...
..81639828352872922..
..73694243721961934..

Quest 17. Given a map with numbers and @ marking a volcano, and a rule for how the volcano “grows”, add up all numbers within radius 10 of the volcano (part 1). The volcano grows in steps, find the step with the highest sum of numbers (part 3). Plan a path from S around the volcano and back to S, given the volcano has grown n steps, each step of the path adds the number and the sum mest be less than (n + 1) * 30. Find n.

In part 1, go through the map and remove all the numbers outside the radius, then add up the remaining numbers. In part 2, visit all numbers. Calculate the step, where this number would be affected, and add the number to a corresponding sum. Find the highest sum. In part 3, Dijkstra! This one I had to think about. In part because the path might visit a number twice. But, there’s a way to do it.

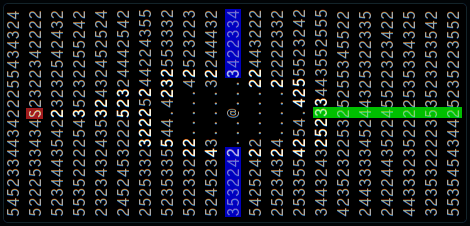
First assume the volcano has grown to radius n. (Beginning with 0.) Then use Dijkstra to find 2 paths, one going clockwise (*) from the red S to a point in the green bar, one counterclockwise. Examine for all points in the green bar. Find the best sum of 2 paths. If it’s too high, calculate the n where this path would have worked, set n to this value and try again. Whew! And I also had to remove my big data structures, when my calculations has finished, or the program would crash.

(*) Force clockwise by removing the lower blue bar.

Plant 1 with thickness 1:
- free branch with thickness 1

Plant 2 with thickness 1:
- free branch with thickness 1

Plant 4 with thickness 17:
- branch to Plant 1 with thickness 15
- branch to Plant 2 with thickness 3

Quest 18. There are plants with branches. Plants like no. 1 can simply be activated. Plants like no. 4 depends on its input from other plants. Given a rule for how plants affect other plants, activate all the simple plants and see how it affects the last plant (part 1). Activate the simple plants using a pattern (part 2). Find the best pattern (part 3).

I had a function to calculate the so called energy for each plant, because I used that code a lot. In part 1 call that function once. In part 2 call it for each pattern. Part 3… For the example data, I could simply try all patterns. But for the notes, a little analysis was required. It turned out, that some simple plants, if activated, would always drag the quality of the pattern down. So, turn on the rest, and boom! Best pattern.

. .......#....#..#........#...#.↑.↑.↑.↑.↑.#.......
9 .......#....#..#...↑....#....↑.↓.↓.↓.↓.↓........
8 ............#..#..↑.↓...#...↑...........↓.......
7 .......↑....#....↑...↓..#..↑............#.......
6 ......↑#↓...#...↑.....↓...↑.............#.......
5 .....↑.#.↓..#..↑.......↓.↑..............#.......
4 ....↑..#..↓.#.↑#........↓...#...........#.......
3 ...↑...#...↓.↑.#............#...........#.......
2 ..↑....#....↓..#............#...........#.......
1 .↑.....#.......#............#...........#.......
↑ S......#.......#........#...#...........#.......

Quest 19. Numbers describe the walls (or rather, the holes in the walls) in a chamber. A rule describes how a duck might fly through the chamber, using the holes. Some of the flight will be flaps upward. Count the flaps (part 1). A wall might have more than 1 hole, find the flight with the lowest number of flaps (part 2 and 3).

There’s recursion involved, because there’s each choice for flap or not flap + the rest of the flight. For small data, trying all choices works fine. For large data… I have a list of the holes. I can calculate the best way to get from a hole to the next. It was fiddly to get this one right. But it’s important to learn. Using sparse data instead of the complete map is a good technique.

T#TTT###T##
.##TT#TT##.
..T###T#T..
...##TT#...
....T##....
.....#.....

Quest 20. A map shows an area with some trampolines. Count pairs of trampolines (part 1). Given 2 points, find the shortest path, jumping between trampolines (part 2). Do it again, but the area is rotating (part 3).

Oh yes. The rotating triangle. But first. Part 1 is very much about interpreting the map correctly. In the top left corner, “T#T” shows a “T#” pair and a “#T” pair. That “#” is also in a pair with a “#” below it, but the “T” on the right is not in a pair with anything below it. Part 2: Convert a Dijkstra to take these pairs into account. Part 3: Implement the rotation. I chose to rotate the jumper. Jump up here, come down there. (Took forever to get right! Better model next time!) And if I come down there, which pairs are available? Wrinkle: I might in essence jump up and down in place. Also, for part 3 I had a more standard graph for Dijkstra. The rotation? Just look at it.

$mn1 = floor($x / 2);
$mn2 = $x % 2;
$m = $mn1 + $mn2;
$n = $mn1;

$op1 = floor($y / 2);
$op2 = $y % 2;
if($mn2 == 0) {
	$o = $op1 + $op2;
	$p = $op1;
} else {
	$p = $op1 + $op2;
	$o = $op1;
}

$new_x = $M - 1 - $n + 2 * $o + $p;
$new_y = $M - 1 - $m - $o;
return [$new_x, $new_y];