This week the #puzzle is: Can You Topple the Tower? #geometry #trigonometry #CenterOfMass #integral

A block tower consists of a solid rectangular prism whose height is 2 and whose base is a square of side length 1. A second prism, made of the same material, and with a base that’s L by 1 and a height of 1, is attached to the top half of the first block, resulting in an overhang as shown below.

When L exceeds some value, the block tower tips over. What is this critical length L?

And for extra credit:

Instead of rectangular prisms, now suppose the tower is part of an annulus. More specifically, it’s the region between two arcs of angle 𝜽 in circles of radius 1 and 2, as shown below.

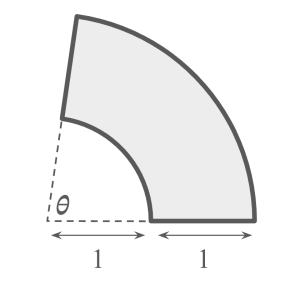For small values of 𝜽, the tower balances on one of its flat sides. But when 𝜽 exceeds some value, the tower no longer balances on a flat side. What is this critical value of 𝜽?

Can You Topple the Tower?

Intermission

Last week I was busy. ( #AdventOfCode ) I misread the description of the puzzle, and by the time I realized my error, I didn’t have enough time left to fix my mistake. So it goes.

Highlight to reveal (possibly incorrect) solution:

Geeks for Geeks Allen Desmos

Thoughts:

• I can look at just 2 of the dimensions and ignore the depth of the block tower.
• Arrange the block tower, so that the tall part has 0 <= x <= 1, and the L part has -L <= x <= 0.
• Method 1.
  • Assume we already know the mass m_i and center of mass (x_i, y_i) for each part of the block tower.
  • x_cm = (m₁ * x₁ + m₂ * x₂) / (m₁ + m₂)
  • The block tower will fall over when x_cm is outside the square base. (We don’t really care about y_cm.)
  • This happens when x_cm < 0.
  • 0 = (L * (- L/2) + 2 * 0.5) / (L + 2)
  • 0 = L * (- L/2) + 2 * 0.5
  • 0 = – L² / 2 + 1
  • 0 = – L² + 2
  • L² = 2
  • L = √2
• Method 2.
  • Let f(x) describe the height of the block tower. For x < 0, this is 1, and for 0 < x, this is 2.
  • x_cm = ∫ x * f(x) dx / ∫ f(x) dx
  • Same result.

And for extra credit:

Thoughts, continued in Desmos.

• Method 2 above can be used again.
• The annulus lies above √(1 – x²) and below √(4 – x²).
• For an angle t, the smaller circle begins at cos(t) and the larger circle begins at 2 cos(t).
• The line segment connecting the 2 circles on the left side is part of the line x * sin(t) / cos(t).
• Putting all this together in Desmos, I get that t = 1.55537, almost π/2.