This week the #puzzle is: Can You Box the Letters? #permutations

In the game of Letter Boxed from The New York Times, you must connect letters together around a square to spell out words. However, from any given letter, the next letter cannot be on the same side of the square.

Consider the following diagram, which consists of eight points (labeled A through H), two on each side of the square. A valid “letter boxed” sequence starts at any of the eight points, and proceeds through all of the other points exactly once. However, adjacent points in the sequence can never be on the same side of the square. The first and last points in the sequence can be on the same side, but do not have to be.

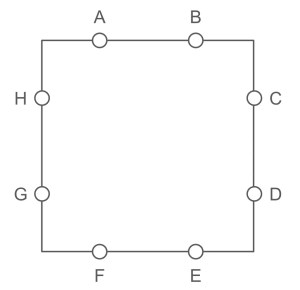As an illustration, AFBCHEDG is a valid sequence of points. However, AFBCHGED is not a valid sequence, since H and G are adjacent in the sequence and on the same side of the square.

How many distinct valid “letter boxed” sequences are there that include all eight points on the square?

And for extra credit:

Instead of two points on each side of the square (and eight points in total), now there are three points on each side (and twelve points in total), labeled A through L in the diagram below.

How many distinct valid “letter boxed” sequences are there that include all 12 points on the square?

Can You Box the Letters?

Highlight to reveal (possibly incorrect) solution:

Spreadsheet Program

Thoughts:

• There are 4 edges, each with 2 letters. Let’s call these edges group 1-4. (Not necessarily meaning group 1 is {A, B} etc.)
• The task is to keep choosing letters, until 0 are left. Also, never choose from the same group twice.

Method 1:

• Choose the 1st letter. There are 8 to choose from. Let’s call this a letter from group 1.
• Choose the 2nd letter. There are 6 to choose from. Let’s call this a letter from group 2.
• Choose the 3rd letter. This could be the remaining letter from group 1, or one of the 4 remaining from unchosen groups. Let’s call the latter a letter from group 3.
  • It was from group 1. Choose the 4th letter. This could the remaining letter from group 2, or one of the 4 remaining from unchosen groups.
    • It was from group 2. Choose the 5th letter. There are 4 to choose from. Let’s call this a letter from group 3.
    • Choose the 6th letter. There are 2 to choose from. Let’s call this a letter from group 4.
    • Choose the 7h letter. It is the remaining letter from group 3.
    • Choose the 8th letter. It is the remaining letter from group 4.
• All this have 8 * 6 * 1 * 1 * 4 * 2 * 1 * 1 = 384 different permutations.
• Of course the full method also investigates all the choices I skipped above. I try to capture all the possibilities in a spreadsheet. Result: 13824.

Method 2:

• Write a program to go through (almost) all options. Same result.

And for extra credit:

Method 2, just with 3 elements in each group. Result: 53529984.