This week the #puzzle is: Fine, Maybe Tiling Problems Can Be Fun… #tiling

Question row A:

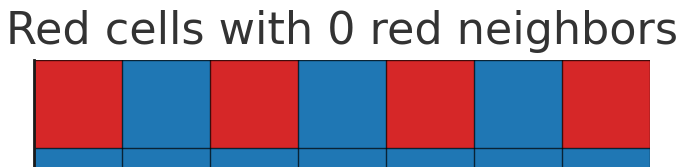
You have an infinite square grid. Each cell in this grid is either red or blue.

Can you create a pattern in which every red cell has exactly:

zero red neighbors, one red neighbor, two red neighbors, ⋮ eight red neighbors?

Neighbors include any cell that is directly adjacent or corner-adjacent. To avoid admitting degenerate solutions, your pattern must have at least some fraction 0<r≤1 of the total board composed of red cells.

Question row B:

Now we will consider patterns in which every red and every blue cell has exactly the same number—nr and nb, respectively—of same colored neighbors. For example, the image above is not a valid pattern since some of the blue cells have 4 blue neighbors while others have 6.

For which pairs (nr, nb) can we construct valid patterns?

Fine, Maybe Tiling Problems Can Be Fun…

Highlight to reveal (possibly incorrect) solution:

Solutions to 1, 2, 3, 4, 5, 5, 6, 7 and 8 neighbors. (Solution for 0 was already given.)

Method: I fooled around with images.

Question row B:

Program

Some more solutions:

nr \ nb	0	1	2	3	4	5	6	7
0	image	image	image	image	image	image	image	(image)
1	image	image	image	image	image	image	(image)	image
2	image	image	image	image	image	image	image	image
3	image	image	image	image	image	image	image	image
4	image	image	(image)	(image)	image	image	image	image
5	image	image	image	image	image	image	image	image
6	(image)	image	(image)	image	image	image	image	image
7	image	image	image	image	image	image	image	image

Thoughts:

• If (n_r, n_b) = (a,b) is possible, (n_r, n_b) = (b,a) is also possible, by reversing the colors.
• If a red has 0 red neighbors, it will have 8 blue neighbors.
  • A blue edge neighbor has at least 4 blue neighbors.
  • A blue corner neighbor has at least 2 blue neighbors.
  • So the cases of (n_r, n_b) = (0, 0), (0,1), (0,2), (0,3) aren’t possible.
  • Similarly for (n_r, n_b) = (1,0), (2,0), (3,0).
• If a red has 1 red neighbor, it will have 7 blue neighbors.
  • A blue edge neighbor has at least 3 blue neighbors.
  • A blue corner neighbor has at least 1 blue neighbor.
  • So the cases of (n_r, n_b) = (1,1), (1,2) aren’t possible.
  • Similarly for (n_r, n_b) = (2,1).
• If a red has 2 red neighbors, it will have 6 blue neighbors.
  • A blue edge neighbor has at least 2 blue neighbors.
  • A blue corner neighbor might have 0 blue neighbors.
  • This does not exclude any new cases.
• Solution with 8 red and x blue can’t work, because there’s no room for the blue. Similarly for 8 blue and x red.
• If a red has 7 red neighbors, it will have 1 blue neighbor.
  • If this is an edge neighbor, it has at most 3 blue neighbors.
  • If it is a corner neighbor, it has at most 5 blue neighbors.
  • So the cases of (n_r, n_b) = (7, 6), (7,7) aren’t possible.
  • Similarly for (n_r, n_b) = (6,7).
• If a red has 6 red neighbors, it will have 2 blue neighbors.
  • A blue edge neighbor has at most 4 blue neighbors.
  • A blue corner neighbor has at most 6 blue neighbors.
  • This does not exclude any new cases.
  • It is however possible to keep building. All the reds have 6 red neighbors. Going through these cases gives a blue cell with at most 5 blue neighbors. (6,6) isn’t possible.
• Method: In some cases I think of a regular pattern, create it and count.
• Further I built a program to create and test patterns. This is how I found the (2, 6) solution.