This week the #puzzle is: Can You Permeate the Pyramid?

Consider the following figure, which shows 16 points arranged in a rhombus shape and connected to their neighbors by edges. How many distinct paths are there from the top point to the bottom along the edges such that:

– You never visit the same point twice. – You only move downward or sideways—never upward.

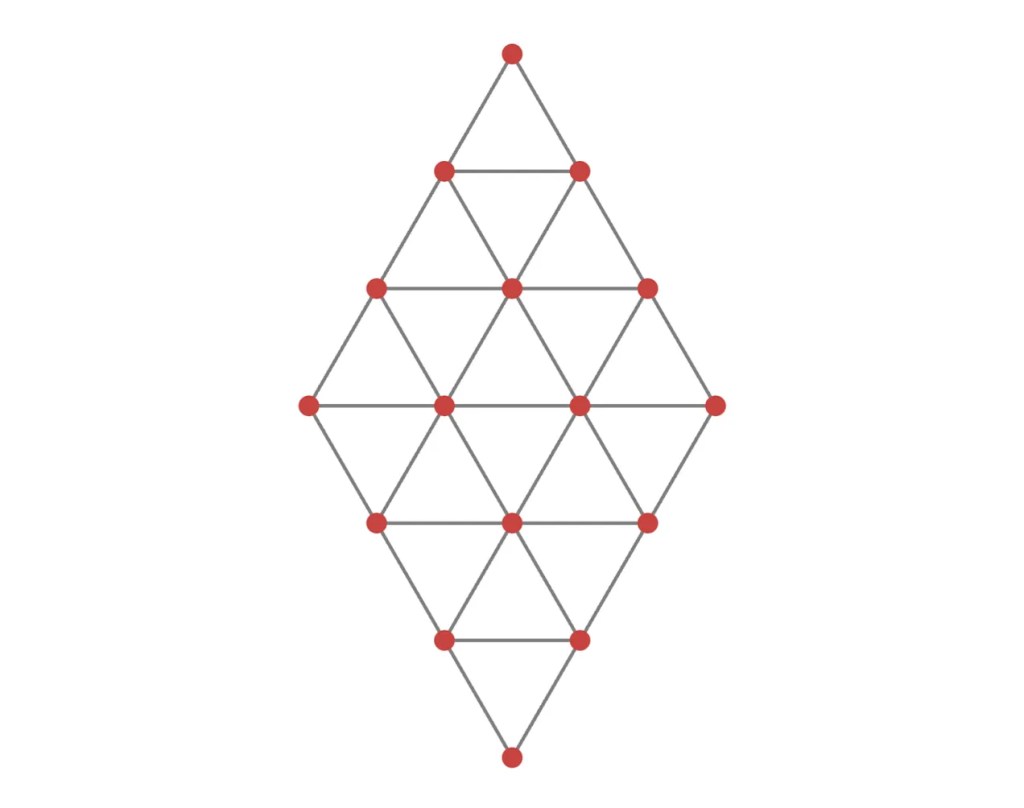And for extra credit:

Consider the following figure, which shows 30 points arranged in a three-dimensional triangular bipyramid. As before, points are connected to their neighbors by edges. How many distinct paths are there from the top point to the bottom along the edges such that:

– You never visit the same point twice. – You only move downward or sideways—never upward.

Highlight to reveal (possibly incorrect) solution:

Program 1.

Let’s number the layers from the top, 1, 2, … 7.

How many paths from layer 6 to 7? Let’s call layer 6 h and i, and layer 7 x.

From h I can go directly to x or through i. For symmetry reasons, i is similar. So, 2 paths from h to x, 2 from i to x. (2 * 2 = 4 in all.)

How many paths from layer 5 to 7? Let’s call layer 5 a, b and c.

From a I can go directly to h or through b. From b I can go directly to h or through a. From c I can go through b to h or through b and a to h. Similarly there are 2 paths from a to i, 2 from b to i and 2 from c to i. When I get to layer 6, there are 2 possible paths to get to x. So, 2 * 2 = 4 paths from a to layer 6, and the same for b and c. All the way from a to x is 4 * 2 = 8. (3 * 8 = 24 in all.)

Let’s write this differently.

Let p(n) be the number of paths from an element in a layer with n elements to layer 7. (Layer 4-7.)

p(1) = 1. There’s only 1 way to do this, stand very still.

p(2) = 2, as we’ve seen.

p(3) = 8 = 2 * 2 * p(2).

In general this is p(n+1) = 2n * p(n).

p(4) = 2 * 3 * 8 = 48.

Now we have to go the other way.

Time to rename the elements.

How many paths from layer 3 to 7? Let’s call layer 3 a, b and c, and layer 4 w, x, y and z.

I can go from a directly to w. From a to x directly or through b. From a to y through b or through b and c. From a to z through b and c. 6 paths from a to layer 4. The same for c.

I can go from b to w through a. From b to x directly or through a. From b to y directly or through c. From b to z through c. Again, 6 paths from b to layer 4.

Let q(n) be the number of paths from an element in a layer with n elements to layer 7. (Layer 1-4.)

q(4) = p(4) = 48.

q(3) = 6 * q(4) = 6 * 48 = 288.

In general this is q(n-1) = 2 * (n-1) * q(n).

q(2) = 2 * 2 * 288 = 1152.

q(1) = 2 * 1 * 1152 = 2304.

q(1) was the number we were looking for. I confirm 2304 is the correct number with a program.

And for extra credit:

Program 2. Program 3. Program 4.

I keep working with the program I wrote earlier. I write versions with 3, 5 and 7 layers. This time I generate the graph by hand. (It’s easier for me to draw it than to write the code.) I also optimize the code a little, only storing the number of paths instead of the paths themselves.

For 3 layers, there are 15 paths. For 5 layers, there are 11,475 paths. (Both of these fit with other programs, I tested out first.) And for 7 layers, there are 1,093,007,025 paths.