This week the question is: Can You Squeeze the Heart?

You can generate a heart shape by drawing a unit square (i.e., a square with side length 1), and then attaching semicircles (each with radius 1/2) to adjacent edges, as shown in the diagram below:

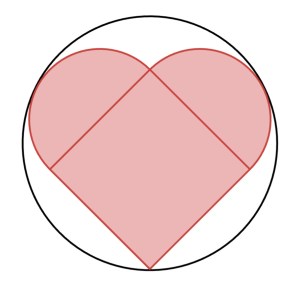
What is the radius of the smallest circle that contains this heart shape?

And for extra credit:

Instead of containing one heart shape, now your circle must contain two heart shapes. Again, each heart consists of a unit square and two semicircular lobes. The two hearts are not allowed to overlap.

What is the radius of the smallest circle that contains these two hearts?

Before moving on to the solutions. Last week I did this:

• Sent in a solution.
• Realized that while the method was right, the numbers ended up being wrong.
• Postponed sending in a new solution.
• Forgot!
• Felt very sorry for myself.

Sigh.

Highlight to reveal (possibly incorrect) solution:

Desmos.

The circumscribed circle passes through the lowest tip of the square. The center of the circle is above that point. I create a simulation in Desmos of the circle, using these 2 items of information. I introduce a variable a for the radius of this circle. I then let a wobble between too small and too large, to get an estimate of a. Zoom into one of the points of the circle, where the wobble is visible, where the circle passes through the tangent point. Repeat. I kept going until I had a between 0.891805 and 0.891806.

And for extra credit:

Figure 1, 2, 3, 4. Desmos 1, 2, 3.

I tried a number on variations on this.

When the 2 hearts point in opposite directions, I can slide them against each other. One configuration is that the 2 squares are neatly lined up, figure 1. Then the radius is a = 1.5. If I slide them “away from” each other, figure 2, a grows bigger. If I slide them “closer to” each other, figure 3, a grows bigger. So if this is indeed the way they are arranged, a = 1.5.

Another option is that the hearts are sort of tucked into each other, figure 4. But again, then a has to be bigger.

The last Desmos attempt looks at one heart right way up, the other tilted 45°. No joy.

There might be other configurations I just can’t think of. Sigh.