A new December and a new bunch of puzzles from mscroggs.co.uk.

Oh goody, time to use my fairly new cross sum skills.

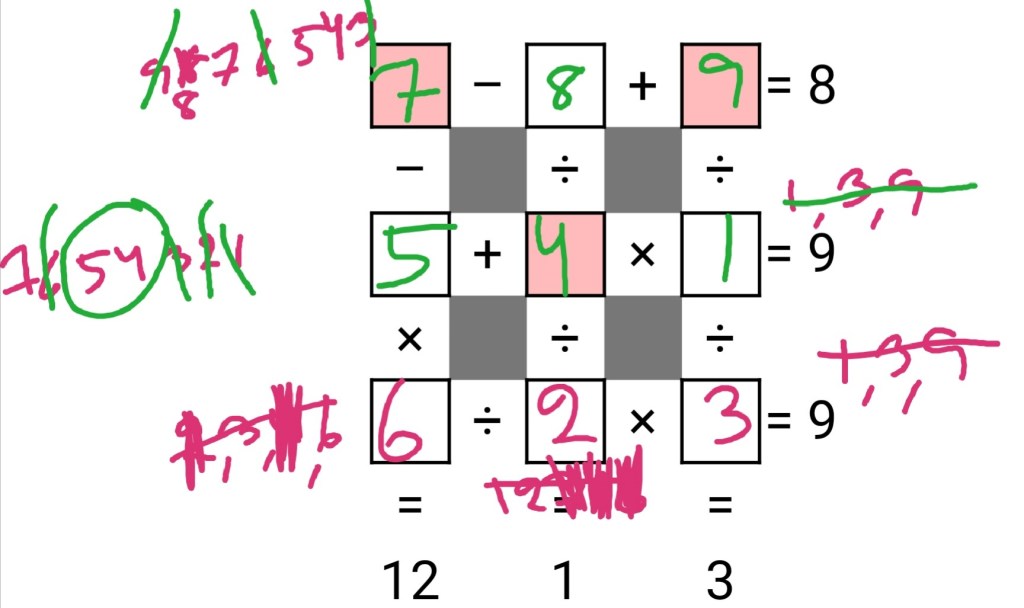
Going left to right, top to bottom, name the boxes a-i.

• R2, C3 (*) = f is an integer dividing 9, therefore one of 1, 3, 9.
• R3, C3 = i, same argument, same result.
• Still R3, C3 = i: the result of a division, c/f, divided by i, is 3. If i = 1, c/f = 3, it’s one of 3/1, 6/2, 9/3. First would require duplication, throw it away. If i = 3, c/f = 9, that would be 9/1. If i = 9, c/f = 27, impossible. New result: one of 1, 3.
• R3, C1 = g is an integer dividing 12, therefore one of 2, 3, 4, 6. (Can’t be 1, that would require the subtraction above, a/d to be 12; can’t be 12, that’s not a digit.)
• R3, C2 = h has to combine with 2, 3, 4, 6 to the left and 1, 3 to the right. g/h*i = 9. g/h must be 3 or 9. 9 is impossible, so it must be 3. Therefore i = 3. Therefore g/h must be 6/2. (It can’t be 3/1 because of duplication.) So g = 6, h = 2.
• Going back to C3, c = 9, f = 1.
• R2, d + e = 9. Of the digits left, it must be 4 and 5.
• R1, a – b = -1. The last digits are 7 and 8. a = 7, b = 8.
• C1, (7-d)*6 = 12. d = 5, e = 4.

(*) Row 2, column 3.

The digits in the boxes are 7, 9 and 4. 7*9*4 = 252.