A new December and a new bunch of puzzles from mscroggs.co.uk.

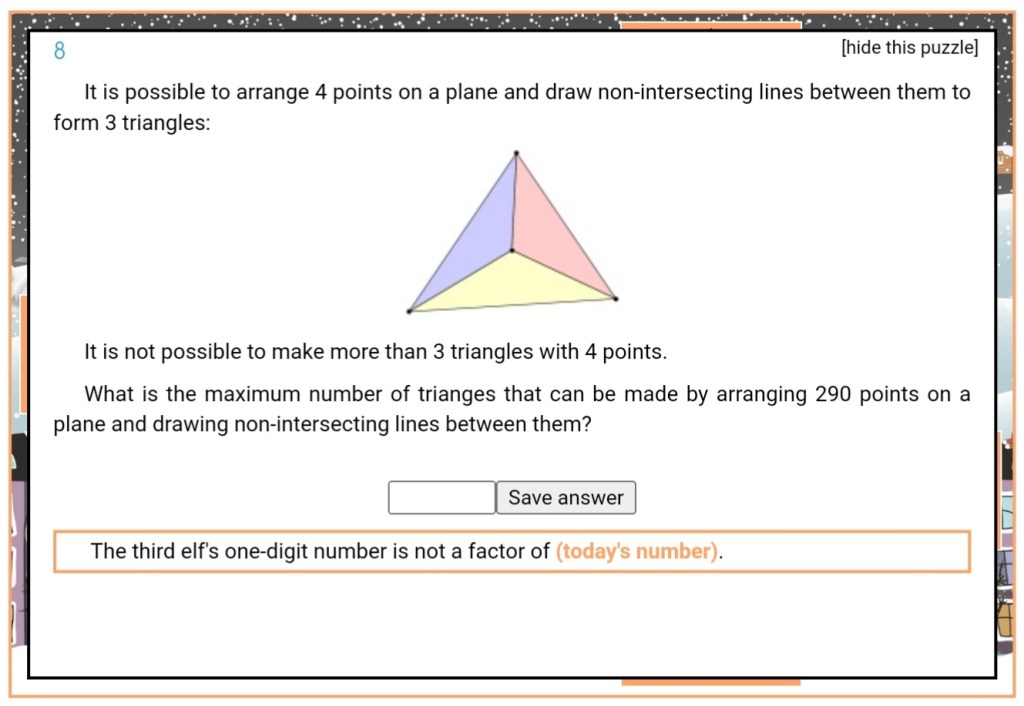
Official answer: “By adding a point inside a triangle, you can turn one triangle into three triangles. By adding a point outside all the current triangles, you can add either one or two more triangles. As we are after the maximum number of triangles, we will choose to add two triangles for each point we add. Four points make 3 triangles. Adding 286 more points will add 572 more triangles, giving a total of 575.”

I think, but I can’t quite prove, the construction of the most triangles possible goes like this:

1. Begin with 2 points and the line between them.
2. Add 2 points close to this and construct the 3 triangles possible.
3. Choose one of the outside lines of the figure.
4. Go back to #2 and repeat.

This means: 2 points, 0 triangles; 4 points, 3 triangles; 6 points, 6 triangles; … ; 2(n+1) points, 3n triangles.

290 = 2(n+1)

145 = n+1

144 = n

432 = 3n

The answer is 432.