This week the question is: Can You Turn a Right Triangle Into an Isosceles Triangle?
Beginning with a 3-4-5 right triangle, it’s possible to append another triangle to one of its sides, thereby making an isosceles triangle. For example, here is how you can make a 5-5-8 isosceles triangle:
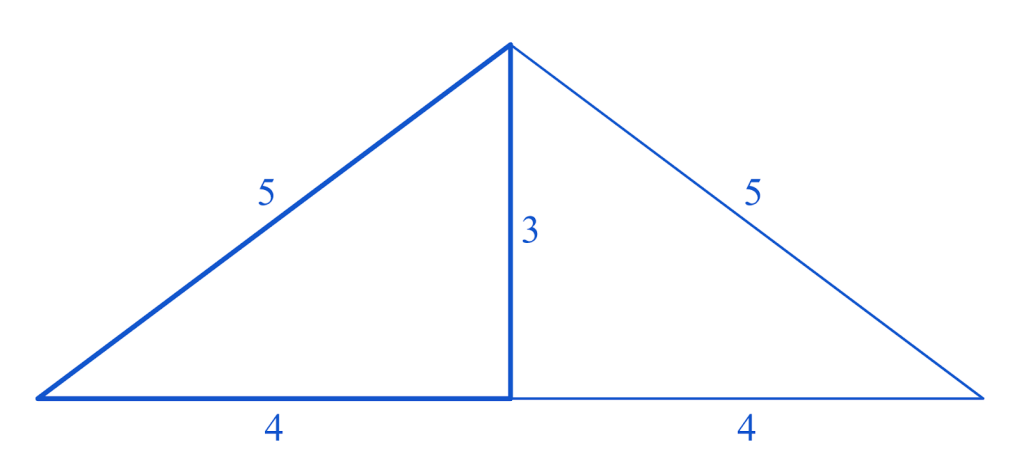
Including the one given above, how many distinct ways can you append a triangle to a 3-4-5 right triangle to make an isosceles triangle?
And for extra credit:
Now suppose you have a right triangle with legs of length a and b and a hypotenuse of length c. And suppose further that there are N distinct ways to append a triangle to this a–b–c right triangle to make an isosceles triangle.
What are all the possible values of N? (Note that any appended triangle may not be degenerate, meaning it must have a positive area. Also, some of the resulting isosceles triangles may be congruent to each other, but they should be counted as distinct if the appended triangles are attached to different sides, or have different positions or orientations.)

ETA: I’m already partially proved wrong.
The first triangle has sides a = 3, b = 4 and c = 5. Opposite side a is angle A etc. Angle C is 90°.
Highlight to reveal solution:
I went around this problem a few times, trying to make sure I had all the possibilities. This is the system, I ended up with.
- A fixed side is also a side, with the same length, in the new triangle. A fixed angle etc.
- I talk about extending a side. This means extending the side to a line and placing a new corner of the new triangle somewhere on the new bits of this line.
- In general, the fixed side has the fixed angle in one end.
- In general, if side x and angle Y are fixed, the extendable side is z.
| Type | Fixed side | Fixed angle | Extending | New triangle sides |
| 1a | c | A | b, right | c, c, 2b |
| 1b | c | B | a, down | c, c, 2a |
| 2 | b | A | c, right | b, b, c+ (long) |
| 3 | c | B | a, down | a+, a+, c |
| 4 | c | B | a, up | b, b, c+ (short) |
By experimenting, I found that all other combinations wouldn’t result in an isosceles triangle. Most of these triangles are illustrated, see above.
Counting, I have found 5 types of triangle extensions.
And for extra credit:
In this case we still begin with a right triangle, but the sides aren’t necessarily 3/4/5. What might happen here? I checked a few cases, and the only interesting one is when a = b. Then we only have type 1a and 1b. So the number of types, N is in {2,5}.
And for super extra credit?
A few triangles without a right angle. This also illustrates travelling on the extended side, looking for a new corner.