This week the question is: How High Can You Jump?

In the high jump, an athlete’s entire body must clear the bar. However, not every part of their body has to clear the bar at the same time. As a result, athletes arc their bodies over the bar, so that only a fraction of their mass is above the bar at any given time. In fact, athletes can theoretically clear the bar despite their center of mass remaining below the bar throughout the jump.

Let’s model the athlete mid-jump as a semicircle, centered over the bar, as shown in the diagram below. For simplicity, assume that their mass is uniformly distributed across the length of their body. The dot in the diagram represents the athlete’s center of mass.

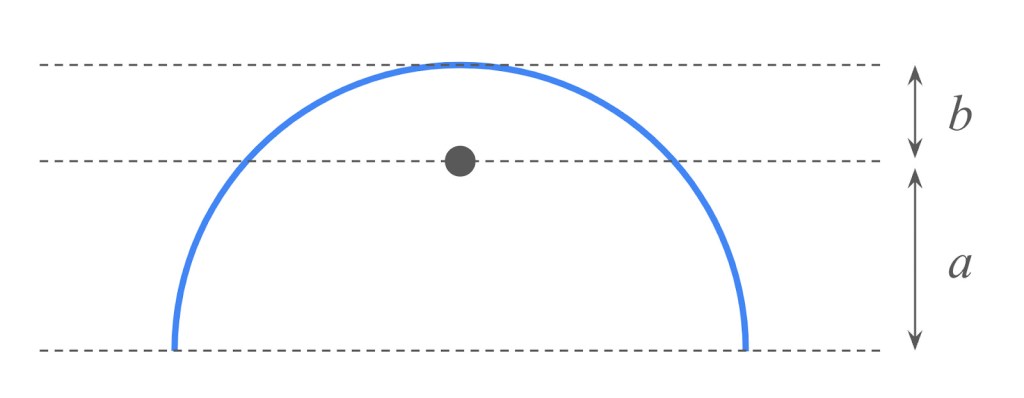
Let a represent the vertical distance between the athlete’s center of mass and their lowest points (presumably their outstretched fingers and toes), and let b represent the vertical distance between the athlete’s center of mass and their highest point (presumably their waist).

What is the ratio a/b?

And for extra credit:

Instead of a semicircle, suppose the athlete’s jump is represented by an arc of angle 2𝜙 that is centered over the bar, as shown below:

As before, a represents the vertical distance between the athlete’s center of mass and their lowest points, while b represents the vertical distance between the athlete’s center of mass and their highest point.

As the angle 𝜙 gets very, very small (i.e., in the limit as 𝜙 goes to zero), what value does the ratio a/b approach?

Læs mere: #ThisWeeksFiddler, 20240816

Highlight to reveal solution:

Helpful Wikipedia page.

So, Wikipedia informs me, that this can be reduced to the case of the “Semicircular arc centroid”. According to that formula, with r being the radius of the semicircle, a = 2r/π and b = r – a = (π-2)r/π. Therefore a/b = 2/(π-2) or approximately 1.75.

And for extra credit:

Calculation sheet.

Wikipedia informs me, this is a case of an “Arc of circle centroid”. The distance from the circle centre to the a line is r*cos(𝜙). The distance between the circle centre and the centre of mass is r*sin(𝜙)/𝜙. Therefore a = r*sin(𝜙)/𝜙 – r*cos(𝜙). Finally, the radius of the circle is r, and b = r – r*sin(𝜙)/𝜙. While calculating a/b, the r cancels out. I ask WolframAlpha for help and get the result 2.