This week the question is: How Many Loops Can You Slither Around?

Nikoli the snake wants to slither along a loop through a four-by-four grid of points. To form a loop, Nikoli can connect any horizontally or vertically adjacent points with a line segment. However, Nikoli has certain standards when it comes to loop construction. In particular:

– The loop can never cross over itself.
– No two corners of the loop can meet at the same point.
– Once Nikoli has crossed the connection between two points, Nikoli can’t cross it again (in either direction).

For example, the following two constructions are valid loops:

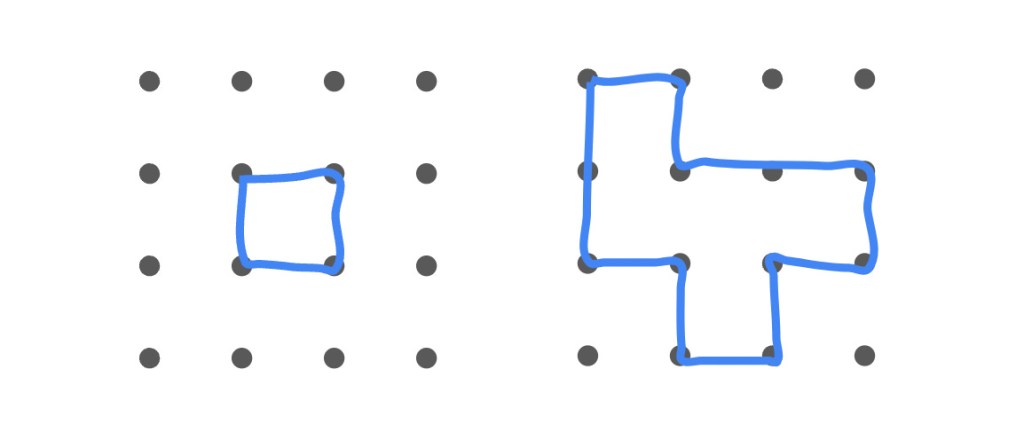
Meanwhile, the following three constructions are not valid. The one on the left crosses over itself, the one in the middle has two corners that meet at a single point, and the one on the right requires Nikoli to pass over the same line segment twice.

How many unique loops can Nikoli make on the four-by-four grid? (For any given loop, Nikoli can travel in two directions around it. However, these should still be counted as a single loop.)

And here’s my suggested solution, highlight to reveal:

Read more: #ThisWeeksFiddler, 20240209

Instead of focusing on the loop, I looked at the squares within the loop. E.g. the first valid loop above encloses one small square, the square in the middle of the grid. If I translate the conditions, I’m looking for a combination of squares, combining into one figure, where all squares are connected side to side. No corner connections, please. I then tried to write all the possible figures down. This is easy enough with 1, 2, 3, 8 and 9 squares. With the rest I got some assistance from Wikipedia, with list of tetrominoes, pentominoes etc.

Once I had my list, for each figure I counted, how many ways it could be placed in the grid. If we look again at the first valid loop above, counting all mirrors, rotations and simple moves, there are 9 versions of this loop.

Here are my figures and counts: 1-5 squares, 6-8 squares and 9 squares.

Adding up all the numbers I get 213 possible loops. (Adding mistake. Got 217 the first time.)