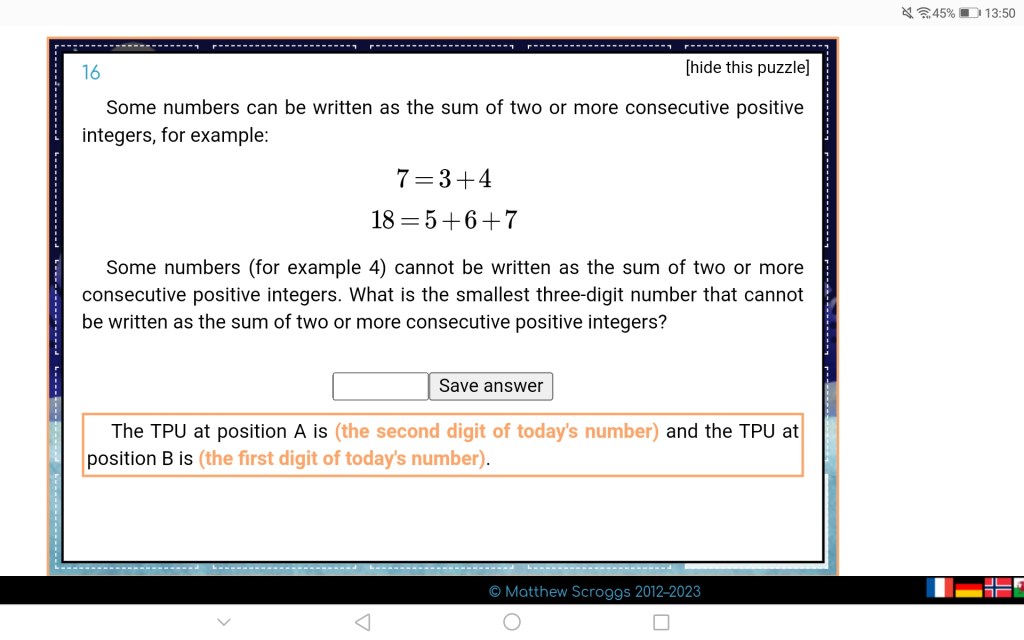
Solution below.

Reveal solution by highlighting:

This one dropped right into one of favourite topics!

An integer can be written as a sum of consecutive integers, if there’s something odd somewhere. Like, 7 = 3+4, because 7 is odd, just like 14 = 2+3+4+5, because 7 (an odd number) is a factor of 14. Why? Because each sum can be written as pairs, each summing to 7: 2+5 + 3+4 = 7+7. On the other hand, the odd number might be hiding somewhere else. 15 = 4+5+6. In this case 5 is the odd number, and besides 5 itself, we can make pairs summing to 2*5. 4+6 + 5 = 2*5+5. But if there’s nothing odd, this can’t be done. In other words, we can’t construct these pairs for the 2ⁿ series. The smallest 3 digit number in this series is 128, the solution.