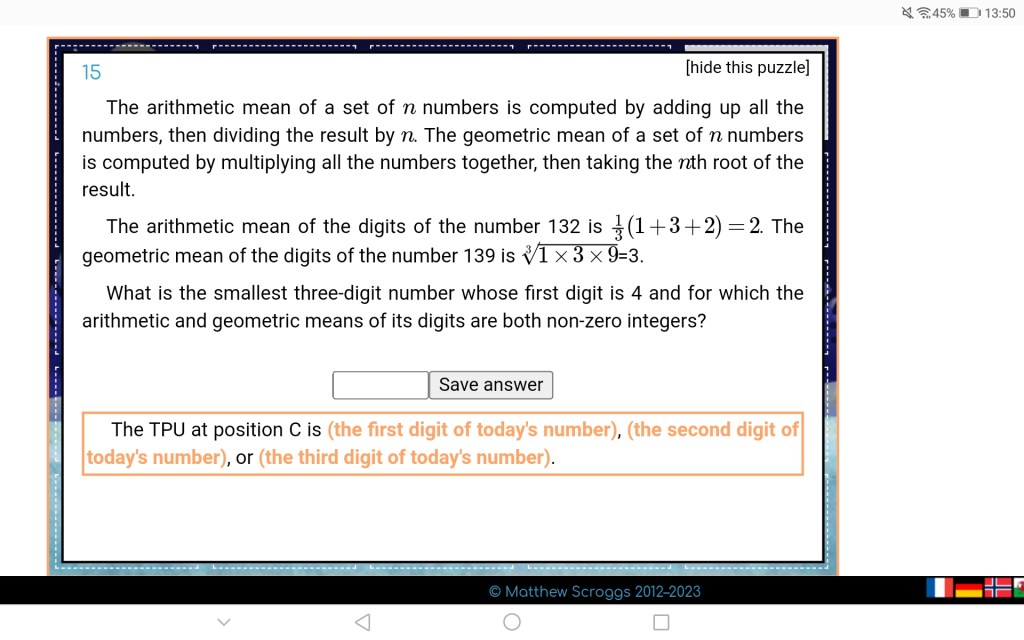
Solution below.
Reveal solution by highlighting:
Our number is 4ab. Both (4+a+b)/3 and (4*a*b)1/3 are nonnegative integers. In particular, this can only be true for the root, if neither a nor b are 0.
For 4*a*b to be a cube, a*b must have 2 as a factor. Let’s just assume a = 2*c. Then c*b must also be a cube number. It might be 1. Then our number is 421, but then the arithmetic mean (AM) isn’t an integer. (Same goes for 412.) Hang on. Let me make a table of all the possibilities. I stop, when the cube gets so big, a and b can’t be digits anymore.
| cube | 2 divides | 4ab | is AM integer? |
| 1 | a | 421 | no |
| same | b | 412 | no |
| 8 = 1*8 | a | 428 | no |
| same | b | n/a | |
| 8 = 2*4 | a | 444 | yes |
| same | b | 428 | no |
| 8 = 4*2 | a | 482 | no |
| same | b | 444 | yes |
| 8 = 8*1 | a | n/a | |
| same | b | 482 | no |
| 27 = 3*9 | a | 469 | no |
| same | b | n/a | |
| 27 = 9*3 | a | n/a | |
| same | b | 496 | no |
| 64=8*8 | either | n/a |
The only possible solution is 444.
Stuff from ommadawn.dk (Lise Andreasen) 