This week the question is: Can You Pack the Circles?

You want to pack four rows of unit circles into a rectangle with a base of 8. You’re considering two strategies for packing:

1. Square packing. In this case, four rows of circles each are packed in an array of squares.

2. Hexagonal packing. In this case, the bottom row has four circles, and higher rows alternate between having three and four circles.

The following diagram shows the square-packed and hexagonal-packed rectangles on the left and right, respectively:

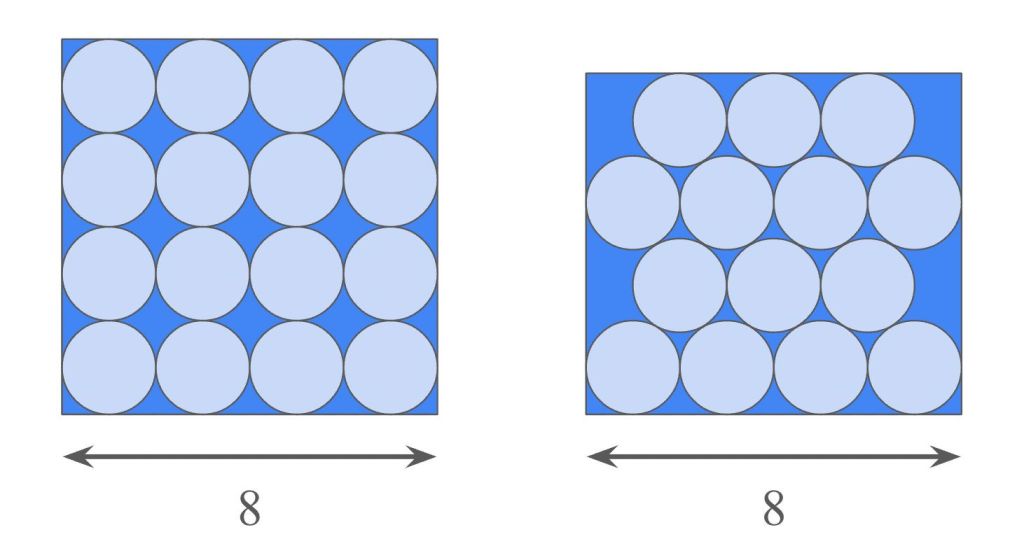
While the bases of both rectangles are 8, their heights are as small as possible such that the circles all fit.

Which packing strategy—square or hexagonal—is more efficient for packing these four rows? In other words, which packing results in a greater number of circles packed per unit of rectangular area?

Læs mere: #ThisWeeksFiddler, 20240614

Highlight to reveal solution:

Calculations, sheet 1 and 2.

I calculate the height of the right rectangle. Then the areas of each rectangle, each set of circles, and I divide. Turns out the left rectangle is more efficiently packed, with 78.5% circles, compared with 76.4% circles. Square packing is better.