| 🇩🇪 Struve | 🇺🇲 Clagett | |
| XVIII, 1 | Form der Berechnung eines Korbes (nb.t), | Example of calculating a basket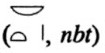 [assumed by Struve as hemispheric in shape] [assumed by Struve as hemispheric in shape] |
| 2 | wenn man dir nennt einen Korb mit einer Mündung (tp-rз) | If someone says to you: “A basket with a mouth opening |
| 3 | zu 4 1/2 in Erhaltung. O | of 4 1/2 (i.e., a diameter of this size) in good condition 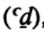 , oh , oh |
| 4 | laß du mich wissen seine (Ober)fläche. Berech- | let me know its [surface] area 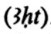 .” .” |
| 5 | ne du 1/9 von 9, weil ja der Korb (nb.t) | [First] calculate 1/9 of 9, since the basket is |
| 6 | die Hälfte eines Eies ist. Es entsteht 1. | 1/2 of an egg-shell (? inr?). The result is 1. |
| XIX, 1 | Berechne du den Rest als 8. | Calculate the remainder as 8. |
| 2 | Berechne du 1/9 von 8. | Calculate 1/9 of 8. |
| 3 | Es entsteht 2/3 1/6 1/18. Berech- | The result is 2/3 1/6 1/18. Cal- |
| 4 | ne du den Rest von dieser 8 nach | culate the remainder from these 8 after |
| 5 | diesen 2/3 1/6 1/18. Es entsteh[t] 7 1/9. | taking away those 2/3 1/6 1/18. The result is 7 1/9. |
| XX, 1 | Rechne du mit 7 1/9 4 1/2mal. | Reckon with 7 1/9 four and one-half times. |
| 2 | Es entsteht 32. Siehe: es ist seine (Ober)fläche. | The result is 32. Behold, this is its area. |
| 3 | Du hast richtig gefunden. | You will find that it is correct. |
Struve:
- … die Berechnung der Oberfläche einer Halbkugel …
- O: die Oberfläche der Halbkugel.
- d: den Durchmesser der “Mündung in Erhaltung”, d.h. der größten Kreises der Halbkugel.
- O = [ (2d – 2/9 d) – 1/9 (2d – 2/9 d) ] * d
- O = 1/2 d π d
- x = π/4 = (8/9)2, Annäherung
- A: Halbkreisumfang.
- A = (2d – 2/9 d) – 1/9 (2d – 2/9 d)
- A = (2d – 2/9 d)(1 – 1/9)
- A = 2d (1 – 1/9) (1 – 1/9)
- A = 2d (8/9)2
- A = 2d x
🇩🇪 Lise:
- Information
- M = 4 1/2, Mündung, Diameter
- O = Oberfläche von Halbkugel (🇺🇲 surface area)
- O = 2 π r2
- r = Radius, M/2
- π/4 = (1 – 1/9)2
- π = 4 (1 – 1/9)2
- O = 2 π r2
- O = 2 * 4 (1 – 1/9)2 (M/2)2
- O = 2 (1 – 1/9)2 M2
- O = 2M (1 – 1/9)2 M
- O = 2M (1 – 1/9) (1 – 1/9) M
- O = (2M – 1/9 2M) (1 – 1/9) M
- O = (2 * 4,5 – 1/9 * 2 * 4,5) (1 – 1/9) 4,5
- O = (9 – 1/9 * 9) (1 – 1/9) 4,5
- O = (9 – 1) (1 – 1/9) 4,5
- O = 8 (1 – 1/9) 4,5
- O = (8 – 8 * 1/9) 4,5
- O = (8 – 8/9) 4,5
- O = 7 1/9 * 4,5
- O = 32
| 🇬🇧 Peet | 🇬🇧 Peet | |
| 1 | Example of working out a semicircle. | Example of working out a semi-cylinder. |
| 2 | If they say to you, A semicircle <of 9> in diameter | If they say to you, A semicircle <of 9> in diameter |
| 3 | by 4 1/2 in height, pray | by 4 1/2 in height, pray |
| 4 | let me know its area. You are to | let me know its area. You are to |
| 5 | take a ninth of 9, since a semicircle | take a ninth of 9, since a semi-cylinder |
| 6 | is half a [circle], result 1. | is half a [cylinder], result 1. |
| 7 | Take the remainder, namely 8. | Take the remainder, namely 8. |
| 8 | You are to take a ninth of 8, | You are to take a ninth of 8, |
| 9 | result 2/3 + 1/6 + 1/18. You are to take | result 2/3 + 1/6 + 1/18. You are to take |
| 10 | the remainder of the 8 after (subtracting) | the remainder of the 8 after (subtraction of) |
| 11 | the 2/3 + 1/6 + 1/18, result 7 1/9. | the 2/3 + 1/6 + 1/18, result 7 1/9. |
| 12 | You are to take 7 1/9 4 1/2 times, | You are to take 7 1/9 4 1/2 times, |
| 13 | result 32. See, this is its area. | result 32. See, this is its area. |
| 14 | You will find it correct. | You will find it correct. |